Journal Information
Title: Enfoque UTE
Abbreviated Title: Enfoque UTE
ISSN (print): 1390-9363
ISSN (electronic): 1390-6542
Publisher: Universidad UTE (Quito, Ecuador)

El análisis mediante el método de elementos finitos, según lo manifiestan Naula, Albuja, Carrillo, e Izurieta (2016), es la vía para dar solución a los problemas de ingeniería, caracterizado por el estudio de modelos matemáticos abstractos, en los cuales intervienen un conjunto de parámetros para predecir fallos en todo sistema físico continuo con un material específico (Vinueza y Gutiérrez, 2018). Xiao, Liu, Du, Wang, y He (2012), lo definen como un método para dar solución a varias incógnitas que se presentan en la ingeniería, donde la resolución involucra varios parámetros de dificultad, cuando se trabaja con geometrías complejas, cargas no distribuidas, cuando están en función de las propiedades de los materiales y porque los resultados analíticos generalmente requieren la solución de ecuaciones diferenciales parciales u ordinarias que no son posibles de resolver (Cubillos, 2015).
La optimización de la topología es una práctica de ingeniería bien establecida para optimizar el diseño de las piezas y crear estructuras livianas y de bajo costo; que históricamente han sido difíciles o imposibles de realizar (Neches, 2015). En el estudio de Meza, Tamayo y Franco (2015), indica que la optimización topológica permite la síntesis de estructuras con valores óptimos de varios de sus parámetros físicos. En relación con las partes mecánicas de bajo peso, implican menores costos por material y menor consumo de combustible en el caso de vehículos de transporte (Silvestre y Robles 2017). En general, la reducción de la inercia en partes de movimiento sea maquinaria o vehículos disminuye la cantidad de energía necesaria para su operación (Powar, Joshi, Khuley y Yesane, 2016).
Se han elaborado análisis topológicos en diversos trabajos utilizando diferentes metodologías para innumerables tipos de piezas mecánicas, que son utilizadas tanto en el área automotriz como industrial y en trabajos de chasis de motocicletas (Powar, Joshi, Khuley, y Yesane 2016), y de la misma manera para el diseño de reducción de material en chasis automotrices Mantovani, Campo, Ferrari, y Cavazzuti (2018). Mediante la utilización de un algoritmo de Meza, Tamayo y Franco (2015), que se usó para rediseñar una pieza mecánica existente, donde la optimización topológica permitió reducción del peso de un 24 %, o el caso de estudio de Ramírez, López y Salazar (2013), que utiliza una metodología donde el área de estudio es un soporte de balancín utilizado en suspensiones automotrices, para minimizar el uso del material, donde se realiza la modificación geométrica de la estructura, utilizando el criterio de distribución de esfuerzos homogéneos permitió minimizar el volumen al 35 % de la estructura inicial, en el caso de Ochoa y Salameda (2013), utiliza la caracterización a través de un estudio de cargas estáticas y dinámicas a partir de resultados y simulaciones computacionales de una pieza automotriz donde se logra reducir el peso del material a un 17.3 %.
El interés del estudio se centra en la importancia que tiene el peso de las autopartes y el significado que representa en el medio de las competencias, en este caso Reyes (2017) argumenta que toda motocicleta que esté relacionada en cualquier tipo de carrera debe contar con un alto rendimiento en términos de aceleración, frenado, manejo y principalmente peso Wang, J., Zhou, J., Li, B. B., Li, X. L., y Song, S. Y. (2012). Además, debe ser lo suficientemente resistente para completar con éxito las etapas descritas de una competencia, los factores de diseño que deben ser considerados tales como: estática, costo, ergonomía, facilidad de mantenimiento, fabricación y fiabilidad.
Por lo expuesto en el presente estudió el objetivo de este trabajo fue determinar si al aplicar una optimización topológica mediante el método de elementos finitos en un chasis de motocicleta de competencia honda CFR230 en condiciones estáticas, los valores de tensión, desplazamiento, deformación unitaria y coeficiente de seguridad están dentro de la tolerancia del material original del chasis. Para lo cual se caracterizará el material del chasis mediante una espectrometría de chispa, se establece el modelo matemático para el análisis estático, se modela y se simula el chasis mediante el software Solid Works Simulation y finalmente se analiza los resultados obtenidos entre el chasis sin modificaciones y el modificado.
El análisis topológico se aplica a diferentes tipos de piezas mecánicas, se ha utilizado en el área aeroespacial, automotriz y obras de infraestructura (Silvestre y Robles, 2017), este trabajo está enfocado en el campo de las competencias, considerando que esta disciplina cada vez tiene más fuerza en nuestro país. El objetivo es optimizar el diseño del chasis de una motocicleta de competencia con un mínimo de peso en comparación al original, de esta manera sea aprovechado al máximo por el piloto.
En lo que se refiere al alcance de este trabajo se lo ha denominado de tipo experimental ya que estudia el problema de manera controlada para una obtención de resultados y su análisis posterior (Bernal, 2016). En este estudio se ha efectuado el análisis del bastidor de una motocicleta de marca y modelo honda CRF 230, de acuerdo con las especificaciones técnicas que se detallan en la Tabla 1, estos son utilizados para el cálculo del análisis estático, de manera específica en valores de dimensiones y pesos, en lo posterior con los resultados obtenidos se podrá establecer las condiciones de frontera, para la elaboración de las simulaciones computacionales.
Fuente: Honda (2013).
Caracterización del material
El elemento que se emplea para la elaboración del estudio, es un material compuesto, según se detalla en la Tabla 2, para la caracterización del material se ha elaborado la investigación en los laboratorios del Departamento de Metalurgia extractiva de la Escuela Politécnica Nacional del Ecuador, utilizando una metodología que trata de un análisis por Espectrometría de Chispa, específicamente se ha utilizado el equipo de denominación Espectrómetro de Marca BRUKER modelo Q4TASMAN, donde se detallan los datos con cifras decimales del porcentaje de cada elemento químico que compone el material.
Al revisar la bibliografía que proporciona Pino (2002), obtenemos el listado de aceros de bajo carbono, en la Tabla 3, se encuentra el material que cumple con los requerimientos químicos aproximados en comparación con los porcentajes químicos del material inicial de la Tabla 2.
Fuente: ESPN (2018).
Fuente: ESPN (2018).
En la Tabla 4 se visualizan las propiedades mecánicas y tecnológicas del material que se va a utilizar, es un SAE 8620 (Aceros al Cromo, Níquel y Molibdeno).
Las propiedades mecánicas de un material son las que se encuentran relacionadas cuando el elemento se somete a esfuerzo, además de la importancia de la utilización de materiales compuestos (Airoldi, A., Bertoli, S., Lanzi, L., Sirna, M., y Sala, G., 2012). En esta investigación para la elaboración de simulaciones se va a trabajar con los valores observados en la Tabla 4, son las caracteísticas mesurables capaces de calificar un comportamiento o una respuesta del mismo a situaciones externas, independientemente del tamaño y la geometría del elemento considerado.
Fuente: Astm (2018).
Cálculo de análisis estático
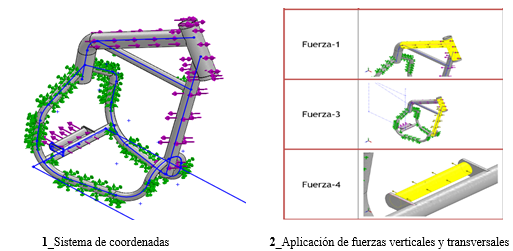
Para establecer las condiciones de frontera y elaborar las simulaciones se necesita los resultados de un análisis estático. Este cálculo se realiza mediante el diagrama de cuerpo libre, con este gráfico se identifica la magnitud y ubicación de las fuerzas que actúan en el bastidor, en la Figura 1(a) y (b) detalla la ubicación y dirección de las magnitudes físicas, estas se identifican mediante una referencia en la revisión bibliográfica de Ochoa y Salameda (2013), este estudio aporta con ecuaciones matemáticas para hallar los valores de los porcentajes de cargas en los ejes delantero y posterior, también los esfuerzos que se encuentran ubicados en cada uno de los puntos establecidos del chasis.
En el diagrama de cuerpo libre que se observa en la Figura 2 (a) y (b), muestra la ubicación y la descomposición de fuerzas, magnitudes físicas y distancias de cada punto en el chasis, se lo ha dividido como horquilla y oscilante.
Es indispensable determinar los porcentajes de cargas en los ejes delantero y posterior ya que son necesarios para hallar los resultados de las fuerzas normales con respecto al suelo y el peso de la moto con el ocupante (hombre), a través del análisis estático, para esto se considera un listado de ecuaciones.
Porcentaje de carga estático en el eje delantero.
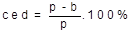 [1]
[1]
Porcentaje de carga estático en el eje posterior.
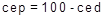 [2]
[2]
Valores de la fuerza normal (eje delantero y posterior) con respecto al suelo y el peso de la moto y el ocupante.
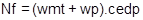
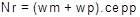 [3]
[3]
Donde:
p
Distancia entre ejes
b
Distancia del CG y eje delantero
wp
Masa ocupante (hombre)
wm
Masa de la Moto
cedp
% de carga eje delantero
cepp
% de carga eje posterior
Nf
Normal eje delantero
Nr
Normal eje posterior
Para determinar los valores del análisis estático, y las fuerzas que actúan sobre los puntos de concentración de esfuerzos se consideran los siguientes cálculos generales (ecuación 4 - 9)
Ecuación para determinar los valores de F1 es la siguiente
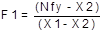 [4]
[4]
Ecuación para determinar los valores de F2 es la siguiente
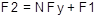
 [5]
[5]
Ecuación para determinar los valores de F3 es la siguiente
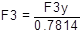
 [6]
[6]
Ecuación para hallar el momento máximo.
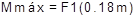
 [7]
[7]
Ecuación para hallar Momento de inercia.}
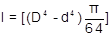
 [8]
[8]
Ecuación para hallar el esfuerzo máximo de deformación.
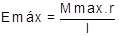
 [9]
[9]
Donde:
X1
Distancia 1 chasis
X2
Distancia 2 chasis
F1
Fuerza 1 Horquilla
F2
Fuerza 2 Horquilla
F3
Fuerza 3 Oscilante
Mmáx
Momento máximo
I
Momento de inercia
Emax
Esfuerzo máximo de deformación
Chasis CAD
Para ejecutar las simulaciones, se ha elaborado la geometría en un programa CAD, por medio de un levantamiento dimensional del bastidor original estándar, el modelo ha sido creado en el software computacional de SolidWorks Simulation, como se puede apreciar en la Figura 3.
Simulación y análisis por elementos finitos
Aplicación de materiales, cargas y soportes
En el proceso de elaboración de las simulaciones se elige el material especificado a todo el cuerpo geométrico para luego aplicar las cargas y soportes en los puntos calculados anteriormente mediante los resultados del análisis estático, se utiliza el sistema de cargas puntuales, en lugares estratégicos del chasis, donde se generan las mayores localidades de esfuerzos, Figura 4.
Selección del mallado
Debido a que la convergencia de la solución depende de la calidad de la malla, es necesario hacer un buen uso de las herramientas de mallado y evitar problemas con el peso computacional (Álvarez, R., Benito, J., Ureña, F., Salete, E., y Aranda, E., 2016). Para el criterio de mallado y generación de elementos de discretización del dominio a través de esta geometría, se ha utilizado un mallado triangular fino, esto garantiza la obtención de datos lo suficientemente precisos para el análisis posterior, observar la Figura 5.
En la Tabla 5 se observan las consideraciones generales de los porcentajes de carga delantero y posterior del bastidor que se ejecutó mediante las ecuaciones (1-2), adicionalmente se obtiene los resultados de las fuerzas normales de los ejes calculados mediante las ecuaciones (3), estos valores se utilizan para hallar las fuerzas que actúan en los puntos de concentración de esfuerzos del chasis.
La Tabla 6 muestra los resultados de las fuerzas ubicadas en la horquilla y el oscilante que fueron obtenidos a través de las ecuaciones (5-9), estas variables ejercen en cada uno de los lugares donde se han considerado que existe mayor cantidad de concentración de esfuerzos. Los resultados van de la mano con los obtenidos en el estudio de Ochoa y Salameda (2013), el comportamiento de las fuerzas aplicadas según los valores obtenidos determinan como está sometido el bastidor en relación al peso del ocupante y de la máquina.
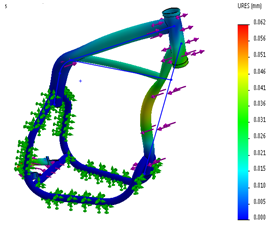
En la Figura 6 (a), se observa los puntos donde existe la mayor concentración de esfuerzos del chasis, en la aplicación de fuerzas tanto en la horquilla y el oscilante del bastidor los resultados que se muestran a través el módulo de von mises da un valor máximo es de 137.36 MPa, la Figura 7 (b) presenta la tabla de desplazamiento con un máximo de 0.062 mm, este valor que se encuentra dentro de las condiciones de diseño, también se considera que la gráfica refleja una escala de deformación de 1053.75.
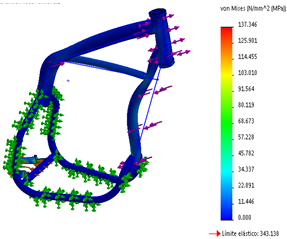
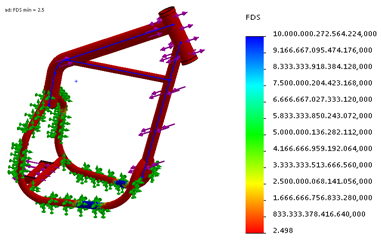
En la Figura 7, se visualiza la gráfica con los valores del factor de seguridad mediante la simulación, este resultado se determina a través de la división del límite elástico del material para el valor de esfuerzo máximo del módulo de von mises, haciendo un análisis en cada uno de los nodos según un criterio de fallos, con un resultado de 2 498.
Aplicación de la optimización topológica en el diseño del chasis
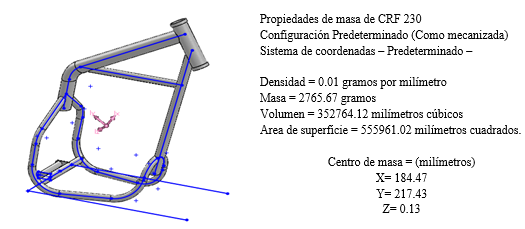
Este método se aplica en base a un criterio de distribución de esfuerzos. El chasis original está diseñado para soportar una carga vertical en la base del amortiguador con un valor de 4003.63 N, y dos cargas diagonales en diferentes sentidos en la horquilla de 2596.989 N y 3294.688 N respectivamente, el material del componente es un Acero de bajo carbono SAE 8620 que cuenta con un límite de fluencia de 343.13 MPa. Usando el programa SolidWorks Simulation, permitió calcular el volumen y la masa del componente inicial antes de la optimización con un valor de 4074.02 g.
Para la aplicación del método de optimización topológica se utilizó una malla fina de 3.7 mm por nodo y con un tamaño de elementos de 608906 mm, a este componente se utilizó un dominio triangular a toda la pieza donde un milímetro equivale a un elemento finito, es decir, tiene una discretización con un total de 97176 elementos finitos (nodos). El dominio posee zonas no optimizables, estas estas ubicadas en las tuberías de menor diámetro de 19 mm que se encuentran ubicadas donde iría el asiento para el piloto.
La topología obtenida se muestra en la Figura 8, sin embargo, la estructura que se obtiene del análisis se muestra de forma difusa, por el motivo que la reducción de material se realizó de forma interna al espesor de los tubos, donde se requiere la interpretación de la geometría para utilizarla en un proceso convencional de diseño mecánico Scappaticci, L., Bartolini, N., Guglielmino, E., y Risitano, G. (2017).
Para verificar que las dos estructuras están dentro de los parámetros de carga (original y optimizado), se ha considerado una comparación de valores con un análisis de distribución esfuerzos mediante el método de elementos finitos con el software comercial SolidWorks, en la Figura 9(a) y (b) muestran la distribución del esfuerzo equivalente del módulo de von mises a través de todo el componente original y el componente aplicado la optimización topológica respectivamente. Donde el valor máximo equivalente de la distribución de esfuerzos de Von Mises para el chasis original tiene un valor de 137.346 MPa. Se observa además que las diversas articulaciones del componente donde indican valores de esfuerzos mínimos, eso representa el material de sobra, el factor de seguridad para el componente original es de 2.498.

El valor del esfuerzo máximo de deformación del chasis aplicando la optimización topológica tiene un valor de 243.25 MPa, estas cargas están ubicadas en lugares estratégicos del chasis, cuenta con un factor de seguridad mínimo de 1.41. La mayor cantidad de material fue removido en las articulaciones del chasis que tienen un diámetro extenso, en esas zonas presentan valores de esfuerzos muy bajos, como se observa en la Figura 10 de tonalidad azul, es ahí donde se puede aplicar la optimización para que los esfuerzos calculados se encuentren dentro de los requerimientos mecánicos del material. Por ejemplo, en el elemento E1 que se tiene un valor inicial del 1.5 mm de espesor a comparación de su valor óptimo máximo resulto ser de 0.75 mm, logrando distribuir la mayor cantidad de material en los lugares que presentan los valores de mayor esfuerzo. Como resultado final de la resultante de nuestro estudio se lo ha catalogado como satisfactorio ya que el valor inicial de masa del componente original es de 4074.02 g fue reducido a 2754.05 g, por lo que se tiene un porcentaje de 67.6 % de reducción.
En la Figura 11, (a) y (b) se observa los Valores de esfuerzo equivalente de Von Mises del chasis original y el chasis optimizado haciendo la comparación de la distribución esfuerzos; obtenemos (a) un valor máximo de 137.346 MPa y en (b) el valor máximo es de 243.25 MPa, ligeramente mayor situado en el mismo punto de concentración del componete original, con la cantidad de material removido de la región del componente donde se presentan los valores de esfuerzo mas bajos.
La segunda parte del análisis es una comparación elaborada mediante el análisis del ingeniero David Vélez Leva en su trabajo de investigación titulado “Diseño, simulación y análisis de un chasis de moto para motor wankel”, este estudio utiliza una metodología de optimización topológica a un chasis de motocicleta, donde se disminuye un 10 % el tamaño de los tubos verticales del bastidor pasando de 25 mm a 18 mm en el diámetro exterior, en el diámetro interior a 22 mm a 15 mm, una vez realizada el análisis del vom mises en los elementos seleccionados se confirma que la modificación es descartada por no satisfacer los criterios establecidos, al obtener un resultado de un aumento de tensión del módulo de von mises de 803.827 MPa a 1179.06 MPa ya que los valores de tensiones superan el valor del límite elástico del material, como se observa en la Tabla 7 se ha elaborado la comparación de los resultados de los dos estudios, en el cual se visualiza que, aplicado la misma metodología los valores encontrados en nuestro estudio están dentro de los criterios de diseño por que los resultados obtenidos están por debajo del valor del límite elástico del material, por otro lado en el estudio Vélez (2014), ha encontrado una solución mediante el diseño de un refuerzo entre los dos tubos verticales con el objetivo de disminuir los resultados de tensión, localizados en los valores extremos del travesaño hasta alcanzar un valor de 741.818 MPa a diferencia del valor inicial de 803.827 MPa.

En la norma del Instituto Ecuatoriano de Normalización (2009), en el punto 5 que trata sobre la Estructura de las Carrocerías, el párrafo 5.1.5.1, detalla que al existir una carga estática sobre la parte superior del elemento, equivale al 50 % del peso máximo admisible para el chasis, distribuido uniformemente a lo largo del mismo, sin experimentar deformaciones en nungún punto; esto lo relacionamos con los valores de nuestro proyecto, las cargas máximas halladas mediante los resultados del programa se obtiene un valor de esfuerzo máximo hallado en el análisis topologico de 243.25 MPa de tensión en el chasis, dividiriamos el limite elástico para el valor máximo de tensión se obtiene un valor de factor de seguridad que resulta 1.41 este valor se encuentra dentro de las tablas del factor de seguridad estático de Supp y Ort (2016), que se muestra en la Tabla 8, los valoremos mínimos de elementos y máquinas que estan sometidos a vibraciones y sin vibraciones, resultado la viabilidad de nuestra investigación.
Para el análisis de los resultados obtenidos de este proyecto se ha resumido en la Tabla 9, se elabora la comparación de valores del chasis original vs el chasis optimizado, garantizando la viabilidad del proyecto.
El chasis de este estudio fue rediseñado con el propósito de eliminar el peso sobrante. Mediante el MEF computacional se generó una estructura óptima con una geometría un poco compleja que fue interpretada para obtener un modelo CAD de la pieza optimizada.
La optimización del diseño que se llevó a cabo en el chasis original consiguió la reducción de masa del elemento mediante la aplicación de un criterio de distribución de esfuerzos donde, el material que se ha eliminado ha sido considerado satisfactorio ya que se permitió calcular una reducción de 4074.02 g a 2754.05 g, equivale al 67.6 % de masa sin comprometer las propiedades mecánicas del material, el factor de seguridad del elemento optimizado que tiene un valor de 1.41, las condiciones de frontera se encuentran dentro de las especificaciones de diseño
El prototipo de chasis de moto se ha diseñado y modelado bajos los parámetros esperados ante las situaciones hipotéticas a las reales a través de los ensayos computacionales, evidenciando el comportamiento mecánico se ha obtenido las máximas tensiones del estudio con un valor de 137.34 MPa del prototipo inicial y de 243.25 MPa del prototipo modificado, resultados que se encuentran por debajo de los valores del límite elástico del material, garantizando un valor del factor de seguridad que se encuentra dentro de los criterios de diseño, frente a las cargas teóricas que se han aplicado sobre la estructura.
Álvarez, R., Benito, J., Ureña, F., Salete, E., Aranda, E., 2016, Introducción al método de los elementso finitos, Universidad Nacional de Educación a Distancia, Madrid, https://www.astmsteel.com/product/aisi-8620-steel-alloy/.
Cubillos, A. (2015). Introducción al método de elementos finitos. https://almec.files.wordpress.com/2007/10/resumen.pdf.
Honda, M. (2018). HONDA Motorcycles. En Honda Manuales. https://honda.com.ec/moto/crf-230f.
Pino, A. (2015). Diagrama de Esfuerzo Deformación. https:m.monografias.com/trabajos72/diagrama-esfuerzo-deformación/diagrama-esfuerzo-deformación.shtml.