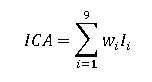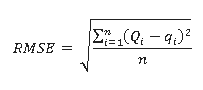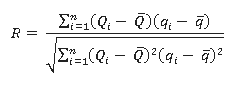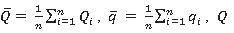1. Introducción
Las aguas superficiales están sometidas a contaminación natural (arrastre de material particulado y disuelto, además de la presencia de materia orgánica natural) y de origen antrópico (descargas de aguas residuales domésticas, escorrentía agrícola, efluentes de procesos industriales, entre otros). El deterioro de las fuentes de abastecimiento de agua incide directamente en el nivel de riesgo sanitario presente y en el tipo de tratamiento requerido para su reducción, por lo que la evaluación de la calidad del agua permite tomar acciones de control y mitigación del mismo, garantizando el suministro de agua segura. Una herramienta común son los índices de calidad de agua (ICA), existe información de que en Alemania, en 1848, ya se realizaban algunos intentos por relacionar la presencia de organismos biológicos con la pureza del agua. En los últimos 130 años, varios países europeos han desarrollado y aplicado diferentes sistemas para clasificar la calidad de las aguas (Torres, Cruz y Patiño 2009).
La RNA es un modelo computacional capaz de imitar las características básicas del cerebro humano como la autoadaptabilidad, autoorganización y la tolerancia a errores. Durante las últimas dos décadas, sus aplicaciones han crecido de manera exponencial en casi todas las áreas de investigación, debido a que permiten resolver problemas que son susceptibles a la estadística convencional, por consiguiente, los modelos que se originan son adecuados para describir pronósticos para tiempos más prolongados, además de relaciones no lineales, por ende, es difícil prescribir la relación matemática exacta entre los parámetros. Se puede resumir, que han sido ampliamente adoptadas para la identificación, análisis, pronóstico, reconocimiento del sistema y optimización del diseño de modelos (López y Fernández 2008).
La RNA perceptrón multicapa (MLP) es un tipo de red, en el que su arquitectura consta de diversas capas, de nodos o neuronas interconectados, cada una de los cuales está conectado a todas las neuronas en la capa siguiente (ver figura 1). La capa de entrada, es en la cual se presentan los datos a la red neuronal, mientras que la capa de salida contiene la respuesta de la red neuronal. Además, posee capas intermedias, denominadas capas ocultas, estas pueden existir entre la capa de entrada y la capa de salida para permitir que estas redes representen y computar complicadas asociaciones entre patrones. Todas las neuronas ocultas y de salida procesan sus entradas multiplicando cada entrada por su peso, sumando el producto, y luego procesando la suma usando una función de transferencia no lineal para generar un resultado. Entre otros, el sigmoide es una de las funciones de transferencia más utilizada (López y Fernández 2008).
Entrenar una RNA es buscar un conjunto de pesos asociados a cada neurona con el fin de que la red pueda, a partir de datos de entrada, generar una salida; en el caso del aprendizaje supervisado, se tiene un conjunto de datos, pero no se conoce la función o relación matemática que los representa. Este proceso es iterativo, en el cual se va refinando la solución hasta alcanzar un nivel de operación suficientemente bueno (Gómez Rojas et al., 2004). La mayoría de los métodos de entrenamiento utilizados en las redes neuronales con conexión hacia delante consisten en proponer una función de error que mida el rendimiento actual de la red en función de los pesos. El objetivo del método de entrenamiento es encontrar el conjunto de pesos que minimizan (o maximizan) la función. El método de optimización proporciona una regla de actualización de los pesos que en función de los patrones de entrada modifica iterativamente los pesos hasta alcanzar el punto óptimo de la red neuronal (Federico Bertona, 2005). En la literatura especializada, encontramos diversos algoritmos con capacidad de entrenar redes neuronales: descenso del gradiente, método de Newton, gradiente conjugado, cuasi-Newton, Levenberg-Marquardt, etc. (Sancho Caparrini, 2017).
Figura 1
(a) Similitudes entre la red neuronal biológica y RNA.
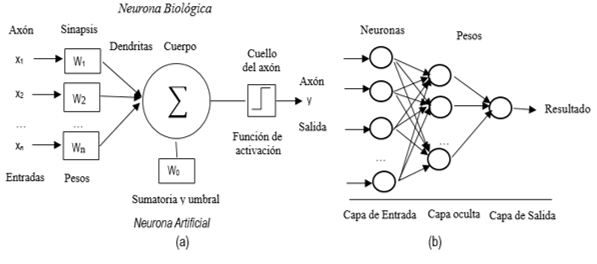
(b) Red perceptrón multicapa.
En este sentido, el empleo de las redes neuronales artificiales en el campo de recursos hídricos se ha vuelto cada vez más usual, es así que se ha propuesto un protocolo sistemático para el desarrollo y la documentación de las RNA, el cual se utilizó para revisar críticamente la calidad de los procesos de desarrollo e informes de modelos de RNA empleados en 81 artículos de revistas desde 2000, en los que la herramienta se ha utilizado para modelar la calidad del agua potable (Wu, Dandy y Maier 2014). Otros trabajos relevantes que se expresan brevemente son: se ha empleado RNA para predecir y pronosticar parámetros físico-químicos y microbiológicos que influyen en la calidad de agua (Chau 2006). Para predecir una variedad de parámetros de calidad del agua en Hilo Bay, Océano Pacífico, donde se aplicaron diferentes combinaciones de parámetros de calidad del agua como parámetros de entrada para predecir los valores diarios de salinidad, temperatura y oxígeno disuelto (Alizadeh y Kavianpour 2015). Modelos de predicción fueron desarrollados para alcalinidad, pH, calcio, dióxido de carbono, temperatura, dureza total, turbidez, sólidos disueltos totales y conductividad eléctrica tienen una capacidad de generalización aceptable, estos modelos pueden ser utilizados por operadores de planta de tratamiento de agua y tomadores de decisiones (Solaimany-Aminabad, Maleki y Hadi 2013). Sin embargo, Thambavani D y Uma (2014) describen el diseño y la aplicación del modelo de MLP de tres capas con alimentación directa y totalmente conectado para calcular el índice de calidad del agua (WQI) para Batlagundu, Dindigul District, Tamilnadu en la India, la arquitectura de red óptima fue 8-3-1, los parámetros de entrada fueron el pH, OD, EC, TDS, TA, TH, Ca, Mg y el algoritmo de entrenamiento fue el de descenso de gradiente. Las RNA se vienen empleando para estimar algún parámetro de calidad de agua de ríos, en función de otros parámetros físico químicos, ver tabla 1.
El objetivo del presente trabajo de investigación fue emplear las redes neuronales artificiales para estimar el índice de la calidad del agua. La red neuronal propuesta emplea herramientas computarizadas, además nos faculta a usar razonamientos aproximados con base en información de campo y previa coordinación con expertos.
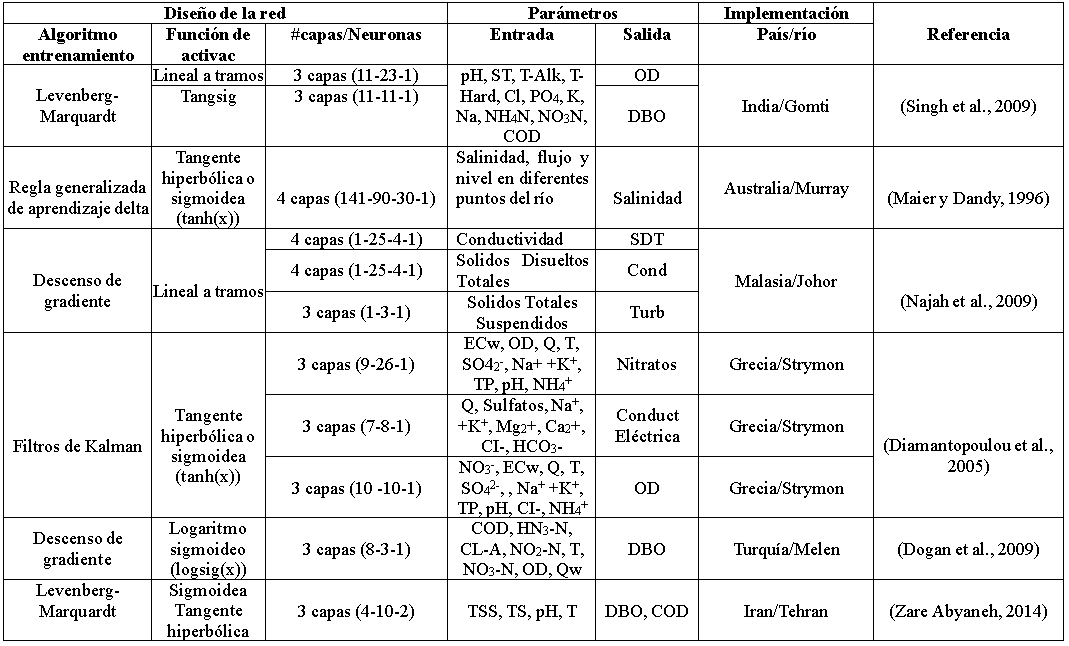
Tabla 1
Diseño entrenamiento e implementación de redes neuronales artificiales perceptrón multicapa empleadas para estimar parámetros de calidad de agua de ríos
Las razones que han motivado a realizar el presente estudio son tres: la primera, desde el punto de vista científico es relevante la validación de un modelo basado en una RNA para estimar un índice de calidad de agua frente a la realidad física que se ha obtenido en estudio previo en la cuenca del río Utcubamba. Segunda, desde el punto de vista funcional, al tener una herramienta computacional confiable en tiempo real para estimar la calidad del agua del río Utcubamba, las instituciones del Estado puede emplearla para realizar operaciones o proponer políticas ambientales que permitan mejorar la calidad del agua, y finalmente, la tercera es emplear modelos de minería de datos, por razones de facilidad de implementación, con un costo relativamente inferior al de los matemáticos como el del índice de calidad de agua NSF WQI, el mismo que necesita más parámetros.
2. Materiales y métodos
Metodología
La metodología empleada fue de tipo analítica y consistió en tres fases: (1) Se recolectó y excluyó data sobre parámetros concerniente a calidad de agua del Río Utcubamba, del Instituto de Investigación para el Desarrollo Sustentable de Ceja de Selva (INDES-CES) de la Universidad Nacional Toribio Rodríguez de Mendoza de Amazonas. (2) Se implementó un modelo que estimó un índice de calidad de agua para el río Utcubamba de la región Amazonas basado en RNA; para este fin se empleó el software Matlab. (3) Finalmente, se validó el modelo, la cual consistió en comparar los residuos obtenidos entre los datos dados por el modelo y los datos recolectados en campo.
Base de Datos para estimar un índice de calidad de agua
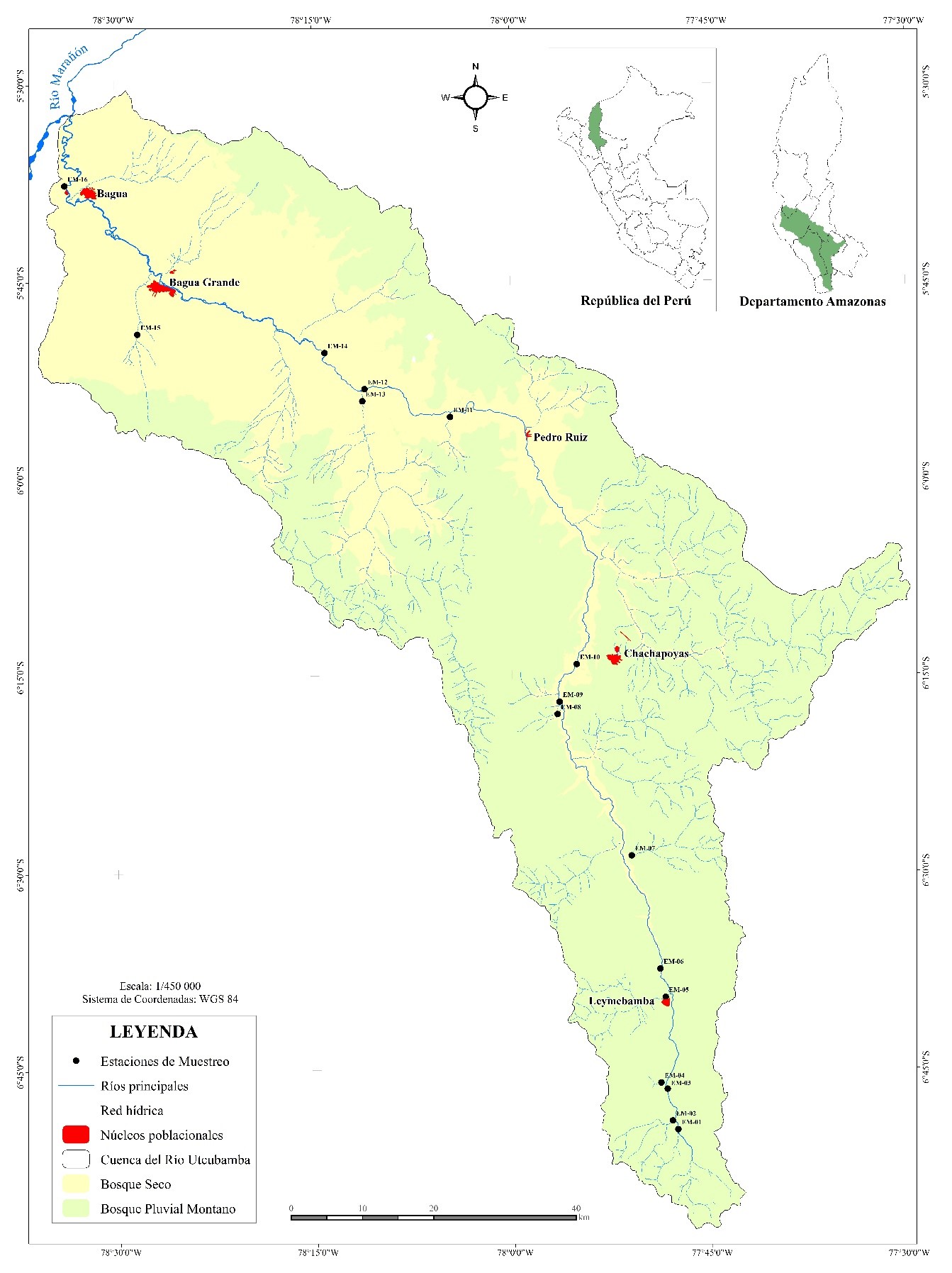
Se realizó una base de datos tomando en cuenta los resultados de los parámetros de calidad ecológica del agua en la cuenca del río Utcubamba, Amazonas, Perú; reportados en la publicación del INDES-CES. Para este estudio previo, la recolección de las muestras de agua se realizó con la estación de lluvias (a lo largo del mes de octubre de 2014), se establecieron cuarenta y tres (43) estaciones de muestreo a lo largo de la cuenca principal y en los tributarios más importantes e influyentes en la misma. Además, para la recogida de muestras para el análisis físico químico (15 parámetros) y microbiológico (4 parámetros) se siguió el protocolo de monitoreo de la calidad sanitaria de los recursos hídricos superficiales, establecido por la Dirección General de Salud Ambiental del Perú, mientras que para el análisis de las parámetros físico químicos y microbiológicas se hizo lo propio con los procedimientos dados en el Standard Methods for the Examination of Water and Wastewater (Gamarra et al., 2018).
La base de datos creada tuvo dos fines, el primero fue determinar el índice de calidad de agua y el segundo fue entrenar, validar y emplear la red neuronal artificial propuesta. Estuvo constituida por 16 instancias concernientes a la misma cantidad de puntos de muestreo; los mismos que fueron considerados debido al tipo de dato ordinal de los diez parámetros tomados en cuenta en el presente estudio, debido a que, para estimar el índice de calidad de agua, se necesitaba este tipo de valores. Cada instancia constó de diez (10) valores, siendo estos: temperatura, oxígeno disuelto, DBO5, sólidos disueltos totales, fosfatos, nitratos, pH, coliformes fecales y turbiedad. En la figura 2, se puede observar la zona de estudio y los dieciséis puntos de muestreo.
El índice de la Fundación Nacional de Saneamiento (NSF WQI)
En Estados Unidos, la Fundación Nacional de Saneamiento (NSF, por sus siglas en inglés) desarrolló el NSF WQI en 1970 mediante el uso de la técnica de encuesta Delphi. Este índice tiene la característica de ser un índice multiparamétrico basado en tres estudios, donde cada una de los nueve parámetros tiene un peso específico de acuerdo con su importancia, relacionada a la calidad del agua. Estos pesos se muestran en la tabla 2, los cuales son aplicados con los parámetros para generar la media ponderada que constituye el ICA (Behar et al., 1997).
El índice NSF WQI fue calculado mediante la ecuación (1), con el propósito de probar la precisión de la red neuronal artificial para estimar el índice de calidad, por lo tanto, en términos de minería de datos, estos datos obtenidos vendrían a ser la verdad absoluta (ground truth).
Tabla 2
Pesos relativos a los parámetros que conforman el NSF WQI
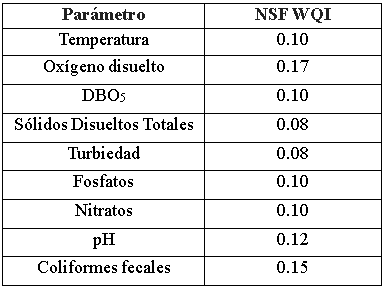
Si denotamos por Ii al subíndice correspondiente a la variable 'I ' y por Wi su ponderación respectiva, el ICA es expresado por:
Ecuación 1 :
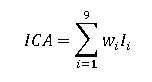
La clasificación de la calidad del agua, empleando el ICA, las cuales se expresan en cinco categorías, dependen del rango numérico dado: Muy mala (0-25), mala (26-50), media (51-70), buena (71-90) y excelente (91-100). Para el cálculo de este índice se utilizó la herramienta de forma online (Water Research Center, 2018).
Figura 2:
Zona de estudio y 16 puntos de muestreo considerados sobre la cuenca del río Utcubamba.
Procedimiento para determinar la arquitectura y validación de la RNA
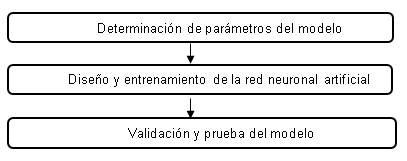
Al emplear una red neuronal, se consideran tres etapas. La primera consiste en el diseño, en el que se elige el tipo de red neuronal a utilizar (la arquitectura o topología), el número de neuronas que la compondrán, función de activación y el algoritmo de entrenamiento. La etapa de entrenamiento, en donde se le presenta a la red neuronal una serie de datos de entrada y datos de salida, para que a partir de ellos pueda aprender, gracias al uso del algoritmo de entrenamiento y, finalmente, el uso que consiste en suministrarles las entradas pertinentes de la red donde esta genera las salidas en función de lo que ha aprendido en la fase de entrenamiento (Dogan et al., 2009). El procedimiento empleado para determinar la arquitectura y validación de la red neuronal artificial, consideró estas etapas, ver figura 3.
Figura 3:
Procedimiento para determinar la arquitectura y validación de la RNA.
Determinación de parámetros del modelo: siete parámetros se han contemplado en la presente investigación. Seis parámetros físico-químicos, los cuales son: oxígeno disuelto y la DBO, debido a que son parámetros químicos de la calidad del agua, nitratos, que es el parámetro que proporciona la información de nutrientes del agua. Además de los coliformes fecales, que es el parámetro biológico que determina el grado de contaminación por microorganismos termo tolerantes, por ende, parte de la calidad sanitaria del agua y, por último, el pH y la turbidez, ya que son parámetros físicos de la calidad del agua, estos parámetros (Srivastava et al., 2013) los propone para estimar un índice de calidad de agua mediante lógica difusa. Por otro lado, otro parámetro contemplado fue el NSF WQI. A fin de evitar impactos negativos en el empleo de la red neuronal es necesario durante la preparación inicial de los datos, estandarizar los datos, es decir, convertir los datos a una forma no dimensional de rango de variabilidad uniforme (Dawson y Wilby, 2001).
La cantidad de instancias de la base de datos disponible para modelar fue de dieciséis, que se asignaron de forma aleatoria en tres conjuntos, denominados de entrenamiento, validación y prueba, la distribución de estos es el 70 %, 10 % y 20 % de los datos ha sido propuesta en el trabajo de May y Sivakumar (2009).
Diseño y entrenamiento de la RNA. El fin fue predecir el estado de la calidad del agua del río Utcubamba (NSF WQI) en términos de seis parámetros físico-químicos, además de considerar los tipos de redes empleadas en estudios previos, ver tabla 1. Este estudio empleó una RNA supervisada y del tipo unidireccional denominado perceptrón de tres capas: La capa de entrada consta de seis parámetros físico-químicos, una capa oculta y el NSF WQI en la capa de salida.
La RNA almacena el conocimiento acerca del problema en términos de pesos en las interconexiones. El proceso de determinar los pesos a la RNA es denominado entrenamiento. La RNA es entrenada con un conjunto de entradas y salidas conocidas. Al principio del entrenamiento, los valores iniciales de los pesos son asignados aleatoriamente. Los pesos son sistemáticamente cambiados por el algoritmo de entrenamiento de forma tal que para una entrada la diferencia entre los resultados de la RNA y los datos actuales son pequeños. Un amplio número de criterios estadísticos están disponibles para comparar la bondad/suficiencia de algún modelo dado. La evaluación estadística del comportamiento usada para el entrenamiento en el presente trabajo fueron la raíz cuadrada media del error (RMSE) y el coeficiente de correlación (R). Estos valores han sido determinados empleando la ecuación (2) y ecuación (3) (Singh et al., 2009).
Ecuación 2:
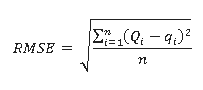
Ecuación 3:
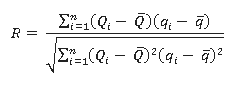
Donde
son los valores observados y q los valores calculados.
Gazzaz et al. (2012) sostienen que el número de neuronas de la capa oculta debería estar dentro del intervalo [1/2, 4I]
, donde I/O es el número de neuronas de la capa de entrada y salida, respectivamente. Por otro lado, Palani et al. (2008) han propuesto que estas neuronas no deberían ser de ninguna manera menor que el máximo de I/3
y O. En nuestro caso, I=6 y O=1. Por ello, remplazando los valores en las ecuaciones, se obtiene que el total de las neuronas ocultas se encuentra dentro del intervalo
El procedimiento que se empleó para obtener la arquitectura óptima de la RNA, fue: (1) Entrenar tres corridas cada red de tres capas, donde las neuronas de entrada fueron 6, de salida 1 y las ocultas cada valor del intervalo [2,24]
, usando el Toolbox del software Matlab, cabe señalar que se utilizó únicamente el conjunto de entrenamiento. (2) Determinar el promedio de los resultados en las tres corridas de los estadísticos RMSE y R, esto debido a que, en la etapa de entrenamiento, se utilizan datos en forma aleatoria para cada corrida. (3) Escoger el número de neuronas que compondría la capa oculta, bajo el criterio que el promedio de R (más cercano a uno) debe ser el mejor y el
el menor, con respecto a todos los promedios encontrados. Estas dos características deben cumplirse al mismo tiempo. (4) La arquitectura óptima de la RNA de tres capas, estuvo compuesta por seis parámetros en la capa de entrada, un parámetro en la capa de salida y la cantidad de neuronas determinadas en el paso (3) en la capa oculta.
En esta etapa, al obtener la arquitectura óptima la RNA es considerada entrenada.
Validación y prueba de la RNA: La validación de la RNA fue realizada mediante dos pasos: (1) Se ejecutaron tres corridas de la red con arquitectura óptima, usando el Toolbox del software Matlab, vale indicar que se utilizó únicamente el conjunto de validación. (2) Determinó el promedio de los resultados en las tres corridas de los estadísticos RMSE y R, esto debido a que, al ejecutar las tres corridas, se utiliza datos en forma aleatoria para cada corrida.
El desempeño o prueba de la RNA se realizó de manera análoga al proceso de validación, con la particularidad que los datos donde se empleará el modelo serán en el conjunto prueba.
3. Resultados
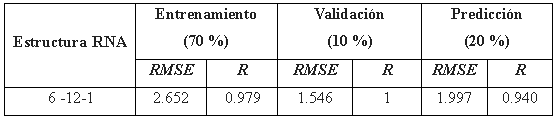
La RNA construida fue entrenada usando el algoritmo de Levenberg-Marquardt, empleó la función de transferencia no lineal (tansig) se utilizó, tanto en la capa oculta como en la externa. Se determinó la distribución óptima, ver tabla 3, consistente de seis neuronas en la capa de entrada, doce neuronas en la capa oculta y una neurona en la capa de salida, el mismo que proporcionó un mejor modelo de ajuste para los tres conjuntos de datos. El coeficiente de correlación (R) para el entrenamiento, validación y los conjuntos de prueba fue de 0.979, 1 y 0.940, respectivamente. Los valores respectivos de RMSE para los tres conjuntos de datos fue 2.562 para entrenamiento, 1.546 la validación y 1.997 la prueba.
Tabla 3
Desempeño de los parámetros de la RNA para estimar la calidad del agua del río Utcubamba Perú
4. Discusión
Los datos que se han utilizado para diseñar, emplear y usar la red neuronal artificial, constó de dieciséis puntos de muestreo del río Utcubamba y sus afluentes, los mismos que fueron sustraídos del trabajo previo, realizado por Gamarra et al. (2018). La recolección de estas muestras de agua se realizó con la estación de lluvias (a lo largo del mes de octubre de 2014).
Se empleó la RNA del tipo perceptrón multicapa para estimar el índice de calidad de agua (NSF WQI), tomando como referencia los trabajos previos (ver tabla 1), considerando como parámetros de entrada a los parámetros: OD, DBO, nitratos, coliformes fecales, pH y turbidez. Diferentes modelos de redes neuronales fueron construidos y examinados para determinar el número óptimo de neuronas en la capa oculta, además de encontrar el porcentaje de distribución óptimo que correspondería a los conjuntos de entrenamiento, validación y pruebas para las muestras.
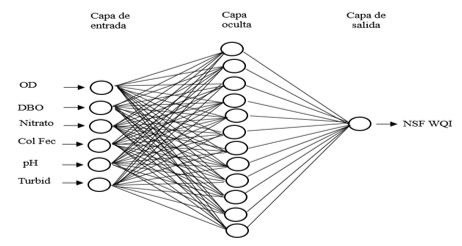
La arquitectura de la RNA óptima para estimar el índice de la calidad del agua de río (NSF WQI) se muestra en la figura 4. Con el trabajo de Thambavani D y Uma (2014), se coincidió en la aplicación del modelo de red neuronal perceptrón de tres capas para calcular el índice de calidad del agua (WQI) para Batlagundu, Dindigul District, Tamilnadu en la India. Sin embargo, existen diferencias con el trabajo mencionado, como la arquitectura de red óptima (8-3-1), los parámetros de entrada, las cuales fueron el pH, OD, EC, TDS, TA, TH, Ca, Mg, el algoritmo de entrenamiento (retro propagación) y el WQI empleado es calculado bajo la normativa del país donde se realizó el estudio.
Figura 4:
Red Neuronal Artificial para estimar el índice de calidad del agua del río Utcubamba (Perú).
Se determinó que la distribución óptima, obteniendo el valor de R mayores que 0.94 y el RMSE menor que 2.65, para la distribución de los conjuntos de entrenamiento, validación y prueba de la RNA, es el 70 %, 10 % y 20 %; esta distribución es la misma encontrada en el trabajo de May y Sivakumar (2009).
5. Conclusiones y recomendaciones
En este trabajo, se propone un modelo basado en redes neuronales artificiales para el cálculo del índice NSF WQI, el mismo que permite determinar el índice de la calidad del agua del río Utcubamba y sus afluentes (Perú). La red neuronal artificial que se empleó ha sido el perceptrón de tres capas, el algoritmo de entrenamiento fue el de Levenberg Marquardt. El presente estudio muestra que la red neuronal artificial óptima que tiene la arquitectura 6-12-1 es capaz de capturar a largo plazo las tendencias observadas a la tediosa variable como es determinar el índice de la calidad del agua (NSF WQI), tanto en el tiempo como en el espacio.
Se destacan a las redes neuronales como una herramienta efectiva para el cálculo del índice de la calidad del agua del río Utcubamba, se concluye que estas podrían también ser utilizadas en otras áreas para mejorar la comprensión del río, tales como las tendencias de la contaminación. La RNA puede ser vista como un poderoso predictor, además de ser otra alternativa a las técnicas de modelado tradicionales.