1. Introducción
El cohete sonda es diseñado para llevar carga útil al espacio, su longitud varía de acuerdo con sus etapas y en cada etapa contiene un motor. Cuando el motor emplea combustible sólido, este se quema en la cámara de combustión a alta presión y temperatura; por tanto, los gases quemados se ven obligados a salir de la tobera convergente-divergente a velocidad supersónica, generando el empuje del cohete.
Cuando el flujo está estrangulado en la garganta, según la presión de escape a la salida de la tobera, el flujo puede estar sobreexpandido, adaptado o subexpandido (Sutton & Biblarz, 2016). Para el flujo sobreexpandido, en la sección divergente de la tobera se presentan ondas de choque normales, oblicuas y de expansión, separación del flujo, cargas laterales y gradientes adversos de presión (Sutton & Biblarz, 2016; Schlichting & Klaus, 2017; Anderson, 2017; Zucker & Biblarz, 2019).
Las formas de las ondas de choque y la separación del flujo de las paredes de la tobera se pueden visualizar por medios experimentales mediante la captura de imágenes con la técnica Schlieren (Dagaro et al., 2019). La turbulencia del flujo (Schlichting & Klaus, 2017) se puede recrear con modelos de turbulencia aplicando la dinámica de fluidos computacional (CFD, por sus siglas en inglés) (Blazek, 2015); y, en la salida de la tobera, el flujo puede ser controlado y manipulado por diferentes mecanismos (Shimshi, et al., 2015; Stark & Génin, 2016;
Kostic et al., 2017).
Diferentes instituciones de universidades de distintos países, tales como Estados Unidos, Alemania, Francia, Polonia, Australia, Japón, China, Italia, España, Corea, entre otros, han centrado su interés en el desarrollo de cohetes sonda con base en proyectos académicos y de investigación (Okninski & Wolanski, 2015; Verberne et al., 2015, 27-29 de julio; Barato et al., 2016, 25-27 de julio; Schüttauf et al., 2017; Huh et al., 2017; Nilsen et al., 2019, 7-11 de enero; Heeg et al., 2020).
En América del Sur, dos países tienen el mayor avance tecnológico, Brasil y Argentina. La Agencia Espacial Brasileña (AEB) ha desarrollado cohetes sonda de varias series y etapas, entre ellos, el VLS es el más emblemático; y algunos cohetes sonda fueron lanzados entre 1965 y 1966 (De Gouyon, 2019). En Argentina, se canceló el proyecto Cóndor (De León, 2016, 26-30 de septiembre). Actualmente, el desarrollo de cohetes sonda está a cargo de la Comisión Nacional de Actividades Espaciales (CONAE). A partir de 2007, lanzaron varios cohetes de la serie Tronador y, a partir de 2014, lanzaron vehículos experimentales suborbitales (Vera, 2015); entre 2015 y 2020 han desarrollado diferentes proyectos en el campo aeroespacial (Schulz et al., 2020). En Perú, la Comisión Nacional de Investigación y Desarrollo Aeroespacial (CONIDA) desarrolló el cohete sonda Paulet I, entre otros cohetes sonda (Canales, 2013, 27 de marzo); en 2004 realizaron diferentes pruebas de lanzamientos de cohetes sondas, así como vienen desarrollando propuestas de modelos de cohetes sonda (Villanueva, 2018, 3-10 de marzo). En Colombia, diferentes universidades están involucradas en el desarrollo de cohetes sonda, tal es el caso del Proyecto Uniandino Aeroespacial (PUA), donde, en 2009, lanzaron el cohete experimental Ainkaa 1 de combustible sólido de 20 kg de empuje; o el desarrollo del cohete sonda Libertador (Morales & Mendoza, 2017).
En la República Bolivariana de Venezuela, en la Universidad de Los Andes (ULA) con sede en el Estado Mérida, se diseñan y construyen cohetes sonda propulsados por motores de combustible sólido, como parte del Proyecto Cohete Sonda Serie ULA que desarrolla la Comisión Rectoral del Programa de Ciencias Espaciales y el Grupo de Ciencias Atmosféricas y del Espacio (GCAE) (Tolentino et al., 2017).
Desde 2006, se han llevado a cabo cuatro pruebas de rendimiento aerodinámico y propulsión de los cohetes sonda ULA-1 y ULA-2, para lo cual, se han hecho diez pruebas en estática de los motores combustible sólido (Parco, 2014). Las toberas diseñadas por la ULA están en su fase experimental, son de geometría cónica convergente-divergente y la garganta tiene una longitud de sección recta determinada, conocida como longitud de garganta.
De la población del grupo de motores de cohetes sonda diseñados por el GCAE, una tobera fue clasificada como ULA-1A XP, la cual fue sometida a ensayos experimentales en un banco de pruebas en estática (Figura 1). Parco (2014) realizó un estudio térmico del flujo en diferentes secciones de la tobera, donde, en la sección de la garganta, la temperatura registró fluctuaciones. Lacruz et al. (2016) llevaron a cabo un estudio de las oscilaciones de la presión interna del flujo en la cámara de combustión, que para ambos casos de estudio es flujo sobre expandido con presencia de ondas de choque en la sección divergente durante los ensayos experimentales.
Sustentados con los datos experimentales de Parco (2014) y Lacruz et al. (2016), Tolentino et al. (2017) hicieron simulaciones numéricas 2D del campo del flujo sobreexpandido para un dominio computacional de la tobera cónica experimental ULA-1A XP. Del estudio numérico, en la sección de la garganta de sección recta de diámetro 15.16 mm y longitud 16.7 mm, obtuvieron ondas de choque oblicuas, donde la velocidad del flujo en ciertas regiones es transónica y en otras, supersónica, por lo cual, el flujo presentó desaceleraciones. En ese sentido, motivó al GCAE a continuar con la investigación.
En el presente trabajo, se simula el flujo en un dominio computacional 2D con simetría axial de la tobera cónica experimental ULA-1A XP para diferentes longitudes de la sección recta de la garganta en el rango de 1-10 mm, con el objeto de analizar numéricamente el comportamiento del flujo en la sección de la garganta. Se presenta el fundamento matemático, el dominio computacional y el método de solución computacional. Se exponen los resultados de los campos de flujo y los perfiles de número de Mach, presión estática y temperatura estática. Posteriormente, se exponen las conclusiones del análisis realizado.
Figura 1
Banco de pruebas en estática
(a) cohete sonda de combustible sólido serie ULA, en la plataforma de lanzamiento; (b) despegue del cohete sonda, (c) motor de cohete sonda de combustible sólido ULA-1A XP, donde, en el extremo derecho del tubo motor, se muestra la tobera cónica acoplada; (d) posición del motor cohete en estática para medir la temperatura (Parco, 2014), y (e) banco de prueba en estática para medir la presión y empuje de los motores de cohetes sonda serie ULA (Lacruz et al., 2016).
2. Materiales y métodos
2.1. Fundamento matemático
En el presente trabajo, la simulación del campo de flujo compresible fue resuelta mediante el modelo de las ecuaciones de Navier-Stokes de número de Reynolds promedio (RANS, por sus siglas en inglés) con el código ANSYS-Fluent v.12.1 que aplica el método de volumen finito (MVF). Las cuatro ecuaciones de gobierno empleadas en el campo de flujo son (1), (2), (3) (ANSYS, 2019) y (4) (Anderson, 2017), las cuales, para las condiciones de flujo en estado estacionario y en forma compacta, se expresan así:
Ecuación de conservación de la masa:
(1) 
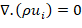
Ecuación de cantidad de movimiento:
(2) 
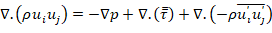
. La ecuación (2) está cerrada, ya que se incluye las tensiones de Reynolds.
Ecuación de la energía:
(3) 
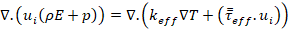
Ecuación de estado:
(4) 
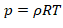
Para flujo compresible, la relación de presiones (5) y de temperaturas (6) en función del número de Mach, ., el cual es el parámetro dominante (Anderson, 2017; Zucker & Biblarz, 2019), se expresan así:
(5) 
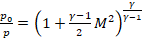
(6) 
(Anderson, 2019).
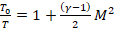
La ley de viscosidad de Sutherland (Anderson, 2017) en función de la temperatura, se expresa así:
(7) 
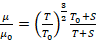
En las simulaciones numéricas, el flujo se consideró como gas ideal. Esto es para el gas que se produce en la cámara de combustión por la quema del propelente sólido compuesto por nitrato de potasio y sacarosa
(Lacruz et al., 2016). Como parámetros, se fijó la relación de calor específico
= 1.4, la constante del gas
= 287J/(kg·K), el calor específico a presión constante
= 1006.43 J/(kg·K) y la conductividad térmica
= 0.0242 W/(m·K). Cabe destacar que la quema del combustible sólido en la cámara no es totalmente homogénea, y esto hace que los parámetros del gas no sean fácilmente medibles, por lo que se tiene que recurrir a la teoría cinética de los gases y del gas real. Por tanto, al considerar un gas homogéneo, facilita el empleo de la ecuación de gas ideal. Además, la viscosidad de diferentes tipos de gases se acondiciona en función de la temperatura, donde Sutherland propuso la ecuación (7), que es ampliamente empleada en códigos computacionales para flujo supersónico.
Para la simulación del flujo, se empleó el modelo de turbulencia de transporte de los esfuerzos cortante SST
de Menter (1994). Este modelo de turbulencia contiene dos ecuaciones: una para la energía cinética específica
, y la otra para la tasa de disipación específica
por lo cual, logra mejorar las respuestas en presencia de gradientes adversos de presión y separación de flujo. Cabe destacar que, previamente, el modelo de turbulencia de Menter fue evaluado por Tolentino & Caraballo (2017), Tolentino (2019; 2020), donde los resultados numéricos se ajustan a los datos experimentales de presión y de velocidad, y es un modelo de turbulencia adecuado para simular la turbulencia del flujo en el presente trabajo.
2.2. Dominio computacional
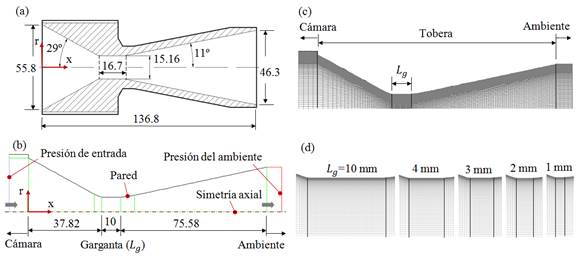
La tobera tónica con longitud de garganta ULA-1A XP, en su diseño original, tiene un ángulo medio de la sección convergente de 29º y de la divergente de 11º, donde las dimensiones básicas se muestran en la Figura 2a. Donde, en la garganta, la relación de longitud y diámetro es
= 1.101.
Para el presente trabajo, se consideraron cinco casos de estudio para la longitud de la garganta, y para la longitud de la sección divergente; se mantiene constante la longitud de la sección convergente de 37.82 mm, así como, valores constantes de los diámetros de la convergente, de la garganta y de la divergente.
Al ser la geometría de la tobera simétrica alrededor del eje
, se consideró simular el flujo para un dominio computacional 2D con simetría axial en el eje
, tal como se muestra el dominio computacional en la Figura 2b. Cabe resaltar que la simplificación de la geometría de 3D a 2D contribuye en la reducción de la cantidad de celdas de la malla, tiempo de procesamiento y coste computacional del equipo, y es muy común las simplificaciones para sólidos de revolución y geometrías simétricas para casos idealizados, donde los resultados no son afectados en las precisiones numéricas de manera significativa con respecto a un flujo en un dominio 3D. No obstante, el dominio 2D tiene su limitación al no permitir proyectar el flujo en la sección transversal, por lo cual un dominio 3D aporta más información para el análisis del flujo cuando se presenta el choque en la divergente. Cabe señalar que en casos idealizados se considera que el flujo es simétrico en la dirección del eje axial, destacando que los estudios experimentales han demostrado que el flujo es asimétrico, como lo reportado por Östlund & Muhammad (2005).
El dominio computacional está compuesto por una sección de la cámara de combustión, la tobera cónica y el ambiente de la atmósfera, donde la longitud de garganta se estableció con medida de
= 10 mm, lo cual corresponde para la longitud de la divergente
= 75.58 mm, como condición inicial. Otros dominios se construyeron para
= 4 mm y
= 69.58 mm;
= 3 mm y
= 68.58 mm;
= 2 mm y
= 67.58 mm, y
= 1 mm y
= 66.58 mm; donde, para el rango de la longitud de garganta 1-10 mm, el ángulo medio se encuentra en el rango de
11.5 a
13.5º; pues, a medida que se disminuye la longitud divergente, el ángulo medio se incrementa al considerar valores constantes para los diámetros de la garganta y de la divergente.
La consideración de una sección de dominio de longitud corta de la cámara de combustión ha sido con el fin de direccionar el flujo cuando se produce la combustión, ya que esta es un tubo largo donde se almacena el combustible sólido, así como la sección del dominio del ambiente de la atmósfera para la descarga del flujo. Además, en el mismo dominio se señala en dónde se aplican las condiciones de borde.
Las condiciones del flujo en la cámara de combustión se establecieron a la presión absoluta de 709 kPa y temperatura de 1673.15 k, basados en los experimentos de Lacruz et al. (2016) y Parco (2014); para el ambiente de la atmósfera, se fijaron a 98 kPa y 293.15 k. Las paredes de la cámara y de la tobera se consideraron adiabáticas y la velocidad del flujo en las paredes se consideró nula por la condición de no deslizamiento. Además, en la simetría axial la velocidad del flujo en la dirección radial es nula. Todas estas condiciones de borde se aplicaron para la tobera con longitud de garganta de 10 mm, 4 mm, 3 mm, 2 mm y 1 mm, respectivamente.
El dominio se malló con malla estructurada con celdas cuadriláteras, el cual fue discretizado por el MVF para
= 10 mm y para las longitudes de garganta de 1-4 mm, las cuales se muestran en las Figuras 2c y 2d. El refinamiento de la malla se aplicó para las regiones adyacentes a las paredes de la cámara y de la tobera, debido a la presencia del esfuerzo cortante en esas regiones.
Figura 2
Longitudes de garganta de 1-4 mm
(a) dimensiones principales de la tobera cónica experimental ULA-1A XP; (b) dominio computacional 2D con simetría axial en el eje x para Importar imagen= 10 mm; (c) dominio mallado con celdas cuadriláteras, y (d) detalles de mallado para los cinco casos de longitud de garganta.
Para el estudio de convergencia numérica, se consideraron tres dominios para la longitud de garganta fija
= 10 mm de la tobera, los cuales fueron mallados en la plataforma ANSYS-Meshing, y se discretizó mediante la interacción de ICEM-CFD. El primer dominio se malló con 18 349 celdas, el segundo con 18 453 celdas, y el tercero con 18 532 celdas. Para los tres dominios mallados, para
= 10 mm, se obtuvo el sesgo equiángulo
≤ 0.22. Cengel y Cimbala (2019) establecen que, para cualquier celda 2D de un dominio computacional, para que la malla sea de buena calidad, el sesgo equiángulo debe estar en el rango de 0 ≤
≤ 1.
2.3. Método de solución computacional
Para la simulación del flujo en el código ANSYS-Fluent, se consideró la opción de solución de análisis basado en densidad para un fluido compresible, y simetría axial 2D. Para la turbulencia del flujo, se optó por el modelo de Menter, y para la viscosidad en función de la temperatura, la ecuación de Sutherland. Para el flujo, la turbulencia de la energía cinética y para la disipación específica, se seleccionó la opción Second Order Upwin. Para el monitor residual, se determinó un valor fijo de 0.00001, tanto para continuidad, velocidad y energía. Se realizaron 35 000-39 000 iteraciones para obtener la convergencia numérica, y se obtuvieron los resultados finales de número de Mach, presión estática y temperatura estática. Para el procesamiento de datos, se utilizó un equipo con las siguientes características: Laptop marca Síragon, modelo M54R, Intel Core 2 Duo, dos procesadores de 1.8 GHz, y memoria RAM de 3 GB.
Ecuación de conservación de la masa:
Importar imagen (1)
Donde la densidad es Importar imagen y la velocidad,
Ecuación de conservación de la masa:
3. Resultados y discusión
3.1. Campo de flujo de número de Mach, presión y temperatura
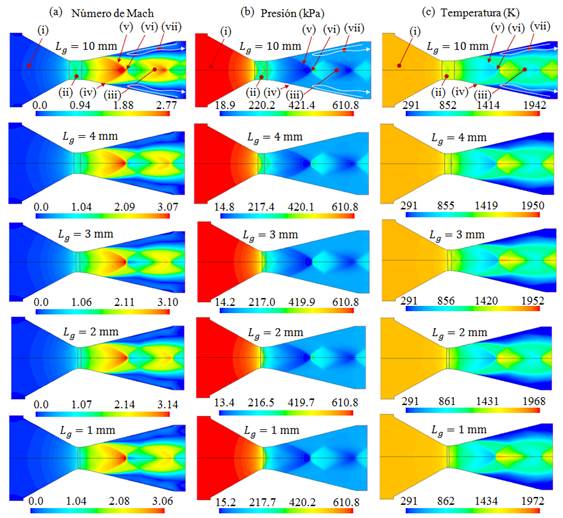
En el dominio del campo de número de Mach (Figura 3a) se observan las regiones donde el flujo es subsónico, transónico y supersónico, así como se muestra en qué regiones sus magnitudes son máximas y mínimas, por medio de la barra de colores. En la sección divergente el flujo está sobreexpandido, lo cual causa separación del flujo de la pared. Se observa en qué regiones del flujo se inicia la separación, así como la recirculación. Para todas las secciones divergentes, las posiciones y las magnitudes de las ondas de choque varían a medida que la longitud de la garganta disminuye, por lo cual, definen un patrón de choque. En la sección de la garganta, para la longitud de la garganta
= 10 mm se aprecia la presencia de una onda de choque oblicua y reflejada, lo cual indica que existe una transición en el régimen del desarrollo del flujo; y a medida que la longitud de la garganta disminuye para
= 4 mm, 3 mm, 2 mm, la presencia de las ondas de choque oblicua se van disipando, y para la longitud de
= 1 mm no hay ondas de choque oblicuas, por lo cual, el flujo para esta longitud no presenta perturbaciones significativas en su desarrollo.
En el campo de presión estática (Figura 3b) se muestran las regiones donde se producen las caídas e incrementos de la presión, y se identifican por medio de los gradientes de la barra de colores de datos donde la presión es máximo y mínimo. Debido al desprendimiento de la capa límite de la pared y separación del flujo de la pared producto de la onda de choque oblicua, se presenta un gradiente adverso de presión en la región de recirculación de flujo con una caída de presión menor a la de la atmósfera local, por tanto, el flujo de aire de la atmósfera local es forzado a ingresar rozando la pared divergente de la tobera.
Así mismo, para el campo de la temperatura estática (Figura 3c), se muestran las regiones del flujo subsónico, transónico y supersónico, y se muestra en qué regiones del flujo la temperatura es mínima y máxima por medio de la barra de colores. Cuando se produce una caída de presión, la temperatura del flujo disminuye, y cuando se incrementa la presión, también se incrementa la temperatura; esto se debe a la naturaleza física del fluido donde la energía interna disminuye a un nivel inferior, consecuencia de la expansión de las moléculas por la disminución de su presión antes de que se presente el choque. Así mismo, después del choque, el flujo es frenado, por tanto, al ser forzado las moléculas a estar más juntas incrementan su energía interna por la resistencia que presentan por el incremento de la presión; en consecuencia, la temperatura se incrementa. Los cambios bruscos de las variaciones de las magnitudes de las temperaturas están presentes en las regiones donde se presenta el choque. De igual manera, en la región donde se presenta la recirculación del flujo, se observa un gradiente de temperatura estática de menor magnitud con respecto a las otras regiones del flujo.
Figura 3
Campo de la temperatura estática
a) campo de número de Mach, (b) campo de presión estática (kPa) y (c) campo de temperatura estática (K). Se señalan para los tres campos de flujo: (i) región subsónica en la convergente, (ii) región transónca en la longitud de garganta, (iii) región del chorro supersónico en la divergente, (iv) inicio de separación de flujo, (v) choque oblicuo, (vi) disco de Mach y (vii) región de circulación de flujo.
3.2. Sección de la garganta: líneas de contorno de número de Mach
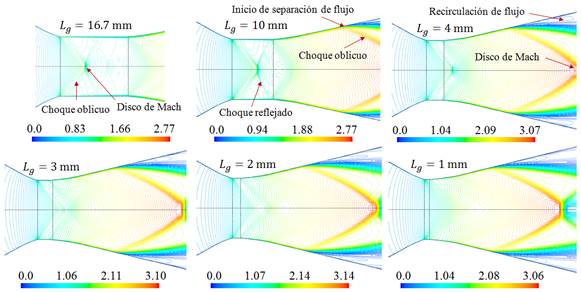
En la Figura 4 se muestran las líneas de contorno para distintas secciones de la garganta con diferentes longitudes. En la sección de la garganta para la longitud de
= 10 mm, se observa una onda de choque oblicuo, la onda reflejada y una onda de choque normal, que es el disco de Mach; así como en la sección divergente se muestra el inicio de la separación del flujo, la recirculación de flujo, el choque oblicuo y reflejado y el disco de Mach. Para el caso de la sección de la garganta, las formas de las ondas de choque son similares a los obtenidos por Tolentino et al. (2017) para
= 16.7 mm, la cual se incluye en la misma figura como referencia (Figura 4a). A pesar de que se ha disminuido la longitud de la garganta de
= 16.7 mm a
= 10 mm, se mantiene casi similar el mismo patrón de comportamiento del flujo en la sección de la garganta.
Para
= 4 mm, el choque reflejado no está presente, solamente el choque oblicuo, y el disco de Mach disminuye su intensidad ubicando su posición en la sección divergente, donde el desarrollo del flujo es diferente al caso anterior, para
= 10 mm. Al disminuir la longitud de la garganta a
= 3 mm, la onda de choque oblicua disminuye su intensidad con tendencia a disiparse y abarca espacio a la entrada de la divergente. Para la longitud de la garganta
= 2 mm, la fluctuación del número de Mach ha disminuido su intensidad drásticamente. Para la longitud de la sección de la garganta de
= 1 mm, se tiene un nuevo patrón de flujo, donde las líneas de contorno muestran que el flujo tiene un mejor comportamiento con respecto a los casos anteriores.
Figura 4
Líneas de contorno de número de Mach para diferentes longitudes de la sección recta de la garganta
3.3. Perfiles de número de Mach, presión y temperatura
Los perfiles de número de Mach, presión estática y temperatura estática evaluados en la simetría axial muestran diferentes patrones, los cuales se aparecen en la Figuras de la 5 a la 7, donde para las Figuras 5a, 6a y 7a corresponden los perfiles para todo el dominio de la tobera, y las otras corresponden para la sección de la garganta y una sección corta de la divergente.
Para el caso del número de Mach, se muestran los valores máximos y mínimos, y en qué distancias de referencias se producen las ondas de choque en la sección de la garganta y en la sección divergente (Figura 5a), por lo cual, el flujo se acelera y desacelera. A medida que se disminuye la longitud de la sección recta de la garganta, las ondas de choque en la sección divergente se producen con mayor intensidad y cambian de posición. Se observa cómo se comporta el flujo en la simetría axial, donde a partir de la distancia estimada entre 43.5 mm a 44 mm se produce una onda de choque normal dentro de la longitud de garganta para
= 10 mm. A medida que la longitud de la garganta disminuye su longitud para
= 4 mm y
= 3 mm, la intensidad de la onda disminuye y se presenta en la sección divergente. Para
= 2 mm, el comportamiento del perfil tiene doble escalón y la desaceleración del flujo es débil aguas abajo, y para
= 1 mm tiene un solo escalón en la sección divergente, y en la sección de la garganta el flujo tiende a acelerarse sin perturbaciones.
Los perfiles de detalles evaluados en la distancia radial, para el tramo en la dirección axial en el rango de 35-60 mm (Figuras 5b-5f), muestran cómo fluctúa la magnitud del número de Mach. A medida que disminuye la longitud de la garganta, el flujo tiende a disminuir su transición, por ende, tiende a acelerarse en ciertas regiones. Para la longitud de la garganta
= 1 mm, el flujo tiene un buen desarrollo y no presenta desaceleraciones, excepto para una región ínfima de flujo adyacente a la pared, esto es, para el perfil de radio 7 mm.
Figura 5
Perfiles de número de Mach para diferentes longitudes de garganta
Los perfiles de presión estática (Figuras 6a-6f) muestran las caídas e incremento de las presiones en las regiones donde se forman las ondas de choques en la sección de la garganta y en parte de la sección divergente. En la dirección radial se muestra el comportamiento de las trayectorias de las curvas y se observa cómo varía la magnitud de la presión, con referencia del eje hacia la pared y en la pared misma, donde para la longitud
= 1 mm, las fluctuaciones han disminuido considerablemente.
Figura 6
Perfiles de presión estática para diferentes longitudes de garganta
Así mismo, las trayectorias de las curvas de temperatura estática (Figuras 7a-7f) evaluadas en la simetría axial y en la dirección radial muestran su comportamiento, se observa que la trayectoria de la curva evaluada en la pared adiabática tiene un valor máximo donde se produce la onda de choque oblicuo, y es un lugar donde se inicia la separación del flujo de la pared, lo cual ocasiona una recirculación del flujo por la caída de presión y, debido a esto, es inducido a ingresar de la atmósfera una porción de flujo de aire rozando la pared interna de la sección divergente, donde el flujo de aire ingresa a la temperatura de la atmósfera local.
Figura 7
Perfiles de temperatura estática para diferentes longitudes de garganta
De los resultados del campo de flujo y de los perfiles, para el dominio computacional de la tobera cónica experimental ULA-1A XP, el comportamiento del flujo es influenciado por la geometría del perfil aerodinámico de la longitud de la garganta. A mayor longitud, se presentan fluctuaciones de los parámetros termodinámicos, por lo cual, se manifiestan las ondas de choque. Los resultados numéricos muestran que para la longitud de la garganta
= 1 mm y
= 15.16 mm se tiene la relación
= 0.0659, donde el flujo presenta un mejor desarrollo y no presenta desaceleración. No obstante, en la divergente de longitud
= 66.58 mm, el cual tiene un valor estimado del ángulo medio ~13.5º, las posiciones de las ondas de choque oblicuas han cambiado de posición, así como se presenta la separación del flujo, los gradientes adversos de presión, y la transición de choque libre (FSS, por sus siglas en inglés) y separación de choque restringida (RSS, por sus siglas en inglés) (Östlund & Muhammad, 2005). El efecto térmico influye en el campo de flujo en la tobera (Ding et al., 2017), sin embargo, en el presente trabajo se ha considerado la tobera con paredes adiabáticas. No obstante, el perfil aerodinámico en la sección de la garganta para relaciones
> 0.1 influye en el desarrollo del flujo en toberas cónicas supersónicas, así como la longitud de la divergente.
Otros estudios experimentales y numéricos en toberas con paredes planas y longitudes variables en la sección divergente han reportado patrones de choques oblicuos en el chorro supersónico (Giglmaier et al., 2014; Nair et al., 2020; Verma et al., 2018; Arora & Vaidyanathan, 2015; Zebiri et al., 2020), por lo cual, a medida que el ángulo medio disminuye, el patrón de choque oblicuo cambia su configuración.
La sección divergente de la tobera con ángulo medio de 15° tiene buen desempeño, y es tomado como referencia en los diseños de las toberas y, típicamente, en diferentes diseños. El ángulo medio de la sección divergente está en el rango de 12° a 18° y es un factor que depende de la aplicación específica y de la trayectoria de vuelo (Sutton & Biblarz, 2016). Además, un factor que se debe tomar en cuenta en la sección de la garganta es el radio de curvatura, lo cual hace que el flujo tenga un buen desarrollo en las regiones adyacentes a las paredes.
Aunque la tobera cónica ULA-1A XP tiene un ángulo medio a = 11º y una longitud de sección recta en la garganta de
= 16.7 mm, con respecto a su diseño original, la tobera ha presentado un buen desempeño en la fase experimental en estática y en dinámica (Parco, 2014; Lacruz et al., 2016), alcanzando los propósitos preestablecidos sobre su diseño; sin embargo, presentó fluctuaciones en la sección de la garganta. La pared de la sección de la garganta de la tobera ULA-1A XP tiene ligeras curvaturas, mas no son curvaturas como de la tobera cónica estudiada por Back & Cuffel (1966), quienes detectaron ondas de choque oblicuas en la sección divergente para un flujo sobreexpandido, para un ángulo medio de la divergente a = 15º.
En el presente trabajo, se ha analizado el comportamiento del flujo en la sección de la garganta para un flujo sobreexpandido para diferentes longitudes de garganta. En el caso de estudio, para un flujo subexpandido para la misma sección de la garganta estudiada de longitud 10 mm, en la sección de la garganta no se presentarán ondas de choque oblicuas, el flujo se desacelerará sin fluctuaciones, luego de salir de la garganta se acelerará, por lo cual, el perfil de velocidad en la garganta presentará un patrón con forma de escalón; este comportamiento hipotético del flujo, de manera similar, fue obtenido por Tolentino et al. (en prensa) para una geometría similar con longitud de garganta para una tobera cónica con relación
= 1.077 y ángulo medio de 15º.
4. Conclusiones y recomendaciones
De acuerdo con los análisis elaborados sobre el comportamiento del campo de flujo en la tobera cónica experimental ULA-1A XP con diferentes longitudes de la garganta, se concluye que:
En la sección divergente se presentan patrones de choque, variando su magnitud y posición por la influencia de la variación de la longitud de la garganta.
En la sección de la garganta, para las longitudes de 10 mm, 4 mm, 3 mm y 2 mm, se presentan fluctuaciones de la velocidad del flujo, con presencia de ondas de choque oblicuo y disco de Mach, que son de mayor intensidad para la longitud de 10 mm; y a medida que disminuye la longitud de garganta hasta 2 mm, las fluctuaciones disminuyen su intensidad. Para la longitud de 1 mm, no se presentan fluctuaciones de los parámetros termodinámicos de velocidad, presión y temperatura, por lo cual, el flujo tiene un mejor desarrollo en su aceleración sin presencia de ondas de choque. Sin embargo, para un valor mayor de
> 0.1, la longitud de garganta influye en el régimen de flujo.
Para trabajos a futuro, se recomienda emplear la misma geometría de la tobera para dominios 2D y 3D y simular para un flujo subexpandido con otros códigos de la CFD y comparar con los resultados de este trabajo.
