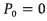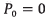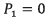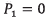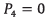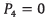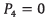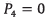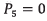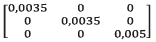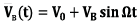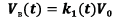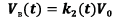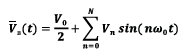Investigation of Wind Effects on UAV Adaptive PID Based MPC Control System

Andrés Santiago Martínez-León1, Sergey Jatsun2, Oksana Emelyanova3

I. Introduction

IN recent decades, the dynamic evolution of information technologies and microelectronics has led to the improvement of modern aviation. This, contributed to rethinking the concepts of unmanned aerial vehicles (UAV’s) use, spheres of their further development, improvement of payload and flight characteristics, hardware-software implementation of promising algorithms of control, among others, all this give to UAV’s a multipurpose character in civil and military fields [1], [3]. Nowadays, fully autonomous small-sized multirotor UAV’s represent a demanded field of research and provide cost-effective solutions for a wide range of applications. This is because their features and ability to carry out operational and high-precision work in hard-to-reach or dangerous areas when performing missions such as search and inspection of remote areas, aerial photography and mapping, agricultural crop monitoring, hazardous material recovery, disaster prevention and relief support or surveillance of sensitive areas (borders, ports, oil pipelines), just to name a few. [1], [2], [4].

Coastal territories constitute a strategic area of interest for any country in terms of trade and responsible natural resource exploitation, also in terms of economic, industrial, political and defense activities in general [4], [5]. However, the presence of coastal territories represents a high responsibility for governmental authorities and implies an accurate control over before mentioned activities by national security services. The coastal territory of Ecuador is no exception, the coastline of the country is characterized by a complex terrain, the presence of hard-to-reach and relatively extended uninhabited territories. This situation is used by some organizations to carry out various types of activities not responding to compliance with law, namely: illegal extraction and trade of natural resources (minerals, petroleum products, wood, poaching, among others.), causing large economic losses [2], [4], [6]. In this regard, maritime security services are constantly in need of expanding and modernizing the technologies used to improve the efficiency of the work carried out to ensure control and safety in these areas. Thus, it becomes necessary to perform remote activities to lead successful interventions along the coastline aimed to identification and detention of members of several illegal organizations, preserving the integrity of the staff of security services [2], [5], [7].

In this paper, the use of a robotic aerial platform is considered to complete remote surveillance missions focused on small sea vessels, as one of the most recurrent means for transporting illegally obtained production. Besides, small sea vessels are difficult to track by standard radar and satellite systems [7]. The proposed aerial platform includes an autonomous small-sized UAV type quadcopter with attachments and a hardware-software system [2], [4], [8], [10].

The peculiarity of monitoring coastal territories belongs to the unpredictability of the air and water environment behavior, as well as the periodic absence of visual contact between the operator and the aerial vehicle when performing remote autonomous missions. Therefore, the robotic aerial platform at least must satisfy conditions such as the use of a lightweight, robust and moisture-resistant UAV frame, based on structural topology optimization principles for better aerodynamics, vibration and payload features [2], [4], [10]. The availability of an energy-efficient system for extended flights, long-range telemetry and video-transmitter modules for real-time flight status management and reception of visual information about ground target identification process respectively. As well as onboard implementation of advanced algorithms of control for an adaptive controlled flight in presence of external uncertainties [4], [7], [8], [9], [13], [19].

The influence of wind loads on the aerial platform can be considered an energy-transfer process, where air and water environment generate additional disturbing forces and momentums of an uncertain nature, which negatively impact on the desired behavior and performance of the aerial platform even at low absolute speeds [2], [9]. Besides, is important taking into account the nonlinearities of the aerial platform, minimal or completely missing information about the environment, external disturbing loads such as swirling wind flows or short-term wind gusts, considered as deterministic or random processes recurring after a certain time or in a certain area, among others. It becomes necessary to work on the implementation of control strategy, which could satisfy properties, including adaptiveness, self-learning, and capability of handling uncertainties during the flight missions performed by the aerial robotic platform [13], [14], [15], [18].

In this regard, the scope of this research work concerns to the investigation and assessment of model-based wind load effects on stabilization and positioning accuracy of the proposed robotic aerial platform operating by an adaptive PID based MPC control system during aerial surveillance missions along the coastline of Ecuador [2]. Thus, the above presented UAV control strategy focuses on a hierarchical control architecture, where the adaptation of PID controller parameters (lower level) and matches the MPC performance (higher level). In this way, the proposed control architecture combines the strengths of PID and MPC methods, minimizing their limitations [2], [19], [23]. Although the implementation of a PID controller provides a simple and accurate control of the UAV electromechanical drives, the efficiency of a PID controller is greatly reduced in presence of uncertainties. Therefore, the use of an MPC control strategy at higher control level by optimizing the PID controller parameters over a certain horizon of prediction and exploiting the knowledge of the UAV dynamic model. It becomes possible to significantly improve the UAV optimal trajectory tracking task, as well as satisfy input and state constraints retaining robust performance, while completing aerial surveillance missions [19], [24].

The aim of this work is related to the implementation of an UAV model-based virtual simulator for investigating the incidence of external uncertainties on the aerial platform flight dynamics for generating the main criteria of a real behavior of the UAV during surveillance missions in coastal region before its implementation. This paper is based on the approaches from previous works [2], [4], namely UAV mathematical model, control and trajectory strategies.

II. Methodology

A. UAV Generalized Mathematical Model

Small-sized multirotor UAV’s incorporate various design configurations. In this paper, it is proposed to use an UAV executed on a quadcopter pattern (cross-shaped scheme). Let’s consider the dynamics of the quadcopter flight in accordance with the given calculation scheme (figure 1). Let the quadcopter motion occur in a global cartesian coordinate system OX₀Y₀Z, then СX₁Y₁Z₁, А_ix_iy_iz_i (i=1-4) – local coordinate systems passing through the center of mass of the UAV C body and the center of mass of the i-th rotor Ai, respectively. The orientation in space is set by the Euler angles of roll j, pitch q and yaw y.

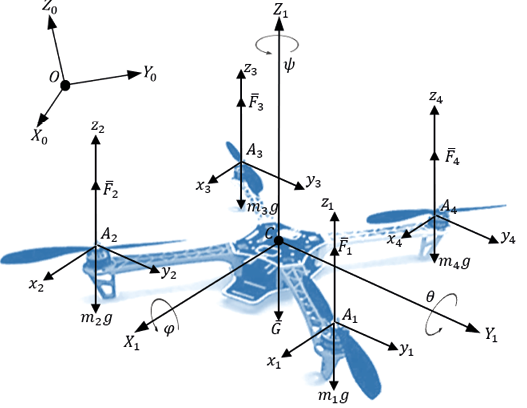
Fig. 1. Calculation scheme of a quadcopter (excluding drag forces).

In general, the motion of a UAV as a solid body involves the motion of the center of mass and rotational motion relative to its center of mass. Consequently, the vector of motion modes (input) of the quadcopter 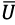, which determines the connection between the electric drives and the quadcopter platform, can be written in the following way [11], [12], [17]:

Equation 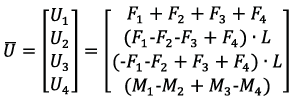1

(1)

Where:

F_i- lifting force of the i-th rotor

Mi - momentum created by the electric drives of the system

L- beams length from the quadcopter center of mass to the i-th rotor platform center of mass

U₁- UAV motion control mode along the vertical axis OZ

U₂ - roll angle φ control mode along the OY axis

U₃ - pitch angle θ control mode along the OX axis

U₄- yaw angle ψ control mode providing UAV rotation around the OZ axis.

Besides, the UAV state vector declaration facilities the calculation of the next states of the aerial platform based on the decoupled dynamic system by using characteristic time step responses for the four controlled states of the UAV according to the output of a designed control system. Thus, the UAV multi-dimensional state vector includes the vectors of position and orientation of the center of mass and respectively. From works [14], [16] the system of differential equations describing the full dynamic model of a UAV type quadcopter (cross-shaped scheme) can be represented as follows:

Equation 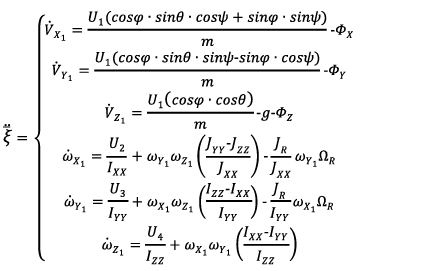2

(2)

Where:

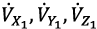and 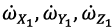- projections of linear and angular accelerations of the quadcopter center of mass on the axes OX₁, OY₁, OZ₁ respectively, φ, θ, ψ - Euler angles, 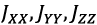- axial momentums of inertia, 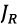- momentum of inertia generated by the electric drives, 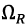- angular velocity of the electric drives, 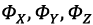- projections of the wind load disturbing force, 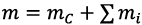- total weight of the UAV.

The presented UAV generalized mathematical model is based on decomposition methods simplifying the complexity of the UAV and contributing to the design of algorithms and synthesis of the control system. Considering equations 1 and 2, is proposed to transform the UAV mathematical model as noted below:

Equation 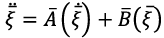3

(3)

Where:

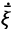- vector of linear and angular velocities of the center of mass of the UAV, 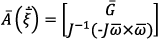- matrix containing the gravitational vector 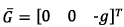and vector of projections of the kinetic momentum on the associated coordinate system, 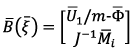- matrix including projection vector of resulting lifting force 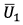, as well as vectors of the external axial momentums 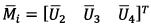and wind load disturbing force .

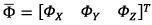In general, the vector of wind load force 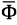describing the effect of external disturbances on the dynamics and stability of the UAV during a flight mission can be represented as follows [14]:

Equation 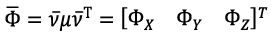4

(4)

Where:

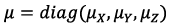- matrix of empirical drag coefficients depending on the aerodynamic characteristics of the fuselage and the angle of attack of the rotors, 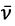- vector of the relative velocity of the center of mass of the UAV.

Then, the vector of relative velocity of the UAV center of mass 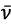can be described as the difference between the vectors of absolute velocity 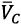and wind load velocity 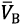[2], [14]:

Equation 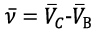5

(5)

However, the rate of change of wind load is a random variable, which can be represented as a trigonometric function with random amplitudes determined by the coefficients of gustiness and the periods of pulsations of the wind load.

B. Wind Load Disturbance Model

During a surveillance mission along coastal territories, the UAVs is quite sensitive to short-term movements of air masses and sea water currents. Moreover, wind load disturbances represent a source of additional forces and momentums acting on the UAV with a complex and unpredictable distribution in space negatively affecting to the static and dynamic stability of the system. In general, wind load disturbances can be directed counter, orthogonally or along the same direction of the UAV movement. In this work, a particular case of orthogonal (lateral) wind disturbance has been considered (figure 2).

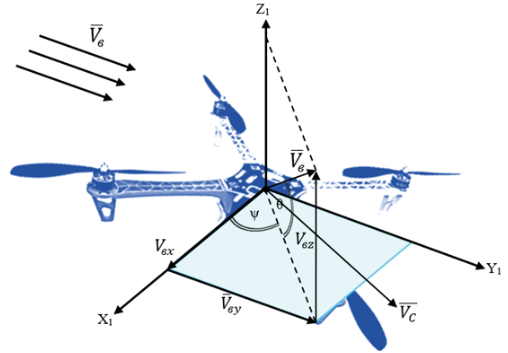
Fig. 2. Scheme of orthogonal wind load disturbance acting on the UAV.

The orthogonal wind disturbance vector 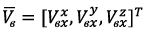is composed of its projections located in the local coordinate system СX₁Z₁. These wind load projections along the axes mostly contribute to significant roll disturbances affecting to the accuracy of the UAV trajectory tracking task, including thrust variation and a higher energy consumption by UAV modules [10], [14], [19].

In addition, wind disturbances can be considered deterministic or random processes that repeat after a certain period (periodic or non-periodic) or occur at a specific time interval (pulse signal). In this work, both mentioned random models are considered.

The modeling process of a random wind load can be described through the next equation [14], [25]:

Equation 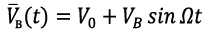6

(6)

Where:

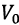- wind constant disturbance, 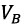, W - arbitrary parameters of orthogonal wind load amplitude and frequency, both resulting from the spectral analysis.

Besides, arbitrary variation of amplitude and frequency parameters is performed by creating time intervals of varying length and generating a continuous random function with a normal (Gaussian) distribution respectively [25].

Equation 7

(7)

Where:

- average value of the wind speed (mathematical expectation), σ - mean square deviation of the wind (variance).

In contrast, wind loads of a deterministic nature (wind shear) often occurs in a relative short time and represent a strong atmospheric disturbance. In this study, the wind shear model is presented by short equation 8 and jump-like equation 9 pulse signals, including a periodic pulse signal in equation 10 modeled by the Fourier series decomposition method [14], [25].

Equation 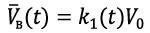8

(8)

Where:

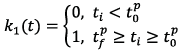- defined function in a certain interval (from the initial time value corresponding to the appearance of the pulse signal 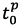to its final value 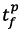at maximum amplitude value of the signal; 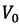- maximum permissible value of the wind load.

Equation 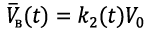9

(9)

Where:

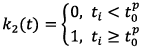- time-dependent switch function; 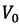- maximum permissible value of the wind load.

Equation 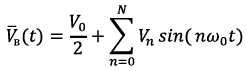10

(10)

Where:

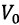- constant of the disturbing effect, 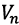- amplitude of the n-th oscillation; 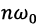- cyclic frequency of the harmonic oscillation.

C. UAV Control System Design

In general, equation 3 presents a compact representation of the UAV generalized mathematical model including kinematic, dynamic and electromechanical components of the system. In order to simplify the design process of the controller of the UAV, the above noted equation is transformed to [2]:

Equation 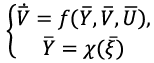11

(11)

Where:

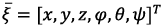- multi-dimensional state vector; 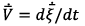- vector of accelerations of the UAV center of mass; 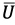- control vector of the UAV motion modes, 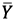- vector of the controlled output signals, 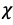- data filtering matrix.

On the other hand, the UAV control system structurally can be presented as a set of the following modules: Operator, Human-Machine Interface (HMI) and UAV (figure 3). In turn, HMI includes the blocks of trajectory planning, data processing and decision-making.

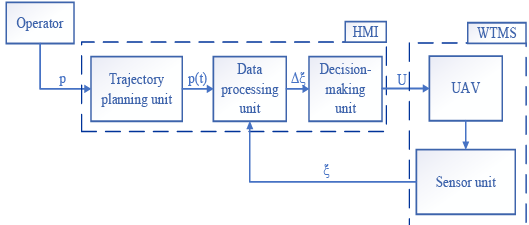
Fig. 3. General diagram of the structure of the UAV control system.

Based on figure 3, the Operator sets an array of GPS coordinates of a specific territory 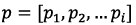. The resulting array data constitutes the input for the trajectory planning unit, where the controlled trajectory law is formed by the vector 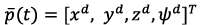. On the other hand, the UAV sensor unit provides accurate feedback of the current state of the system turning possible to estimate the error vector 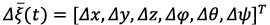. In this way, the output vector of the UAV controlled states 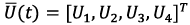is generated considering the system current information and algorithms embedded in the decision-making unit. As presented in introduction section, the design of the UAV controller focuses on a hierarchical architecture, where the adaptation of the PID controller parameters in presence of probabilistic uncertainties is performed by the prediction of the plant response at every sample k to enhance the desired behavior over a prediction horizon N using a robust MPC controller [2], [14], [23], [24]. Moreover, the adaptation of controller parameters aims to overcome the PID algorithm limitations implementing an online tunning method given by MPC algorithm, which leads to lower complexity and computations. In figure 4, the internal structure of the decision-making block is presented. According to this diagram, two control loops based on the use of the PID controller are distinguished: an external loop for controlling the x, y coordinates; an internal loop providing control of height z and UAV angles φ, θ, ψ.

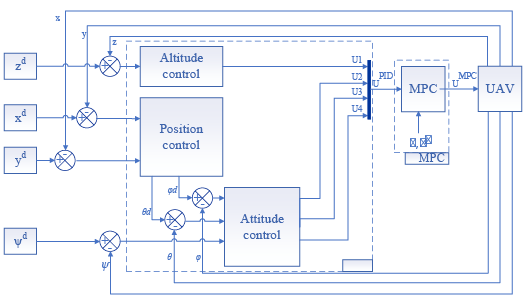
Fig. 4. Internal structure diagram of the UAV making-decision unit.

The implementation of the method for synthesizing the parameters of the UAV control system is performed according to the presented diagram in figure 4. The formation of the output vector of the UAV controlled states 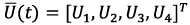is carried out based on available information about the system and embedded algorithms in the decision-making unit. This vector establishes the relation between the electric drives and the UAV current states. On the other hand, the estimation of the vector of required voltages 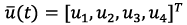is generated in accordance with the output vector . In this way, the vector of required voltages 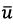depends on the deviation vector of controlled states 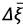. In this regard, the UAV angular velocity generated by the electric drives is represented as follows [17]:

Equation 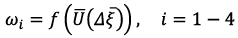12

(12)

Where: 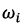- angular velocity of the n-th electric drive.

In general, the generation of controlled states of the output vector 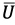can be described in a matrix form:

Equation 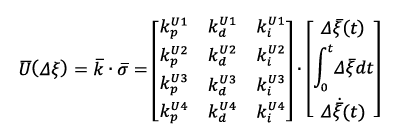13

(13)

Where:

- matrix of proportional 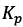, integral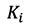and differential coefficients of each controlled state of the output vector 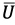; 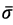- matrix containing the estimation of the deviation of the state vector 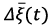, its integral 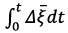and differential 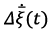components respectively.

In figure 5, the internal structure of the MPC control unit is presented. The prediction of the elements of the output vector 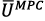is obtained by solving an optimization task within a certain prediction horizon N (time interval).

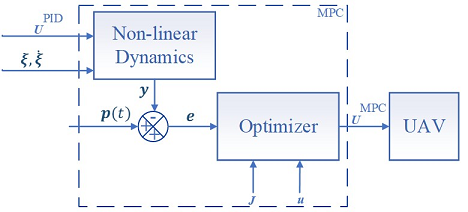
Fig. 5. Internal structure diagram of the MPC control unit.

The nonlinear system describing the dynamics of the UAV is solved by the Euler integration method and can be represented as:

Equation 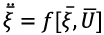14

(14)

Where:

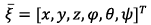- multi-dimensional state vector, 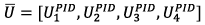- vector of the control signals requiring optimization.

The mathematical significance of the MPC control algorithm synthesis belongs to form a vector of predictive output signals of the UAV for a certain number of iterations ahead within a given prediction horizon based on the ideal dynamic model of the UAV [19], [23].

Equation 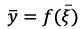15

(15)

Where: 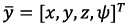- vector of predicted output signals of the control object.

Thus, the deviation vector 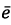between the predicted 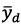and specified by the operator 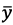trajectories can be determined as noted below:

Equation 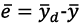16

(16)

Besides, the quality functional 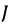can be considered as a quadratic sum function of accumulated deviations of the predicted output vector .

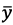Equation 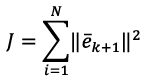17

(17)

Further, the optimization task is carried out by calculating the quality functional 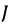according to the quadratic programming algorithm (figure 6), based on predictive models considering system constraints 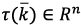for the estimation of the optimized output vector .

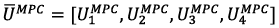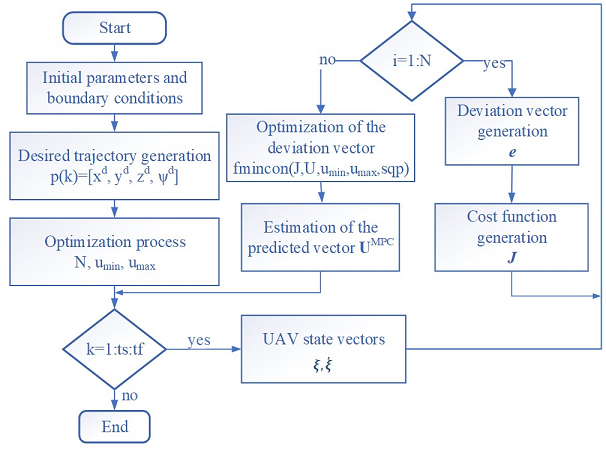
Fig. 6. Diagram of the MPC algorithm for UAV trajectory tracking optimization.

D. UAV Surveillance Trajectory Design

In figure 7 is described a particular case of the surveillance trajectory. The spatial motion of the UAV can be considered as a set of straight-line segments forming a piecewise linear trajectory. The controlled trajectory motion is represented by the displacement of the point P (center of mass of the UAV) along a straight-line segment . Besides, it is necessary to consider the possibility to perform an open (along the coastline with a subsequent landing process at an intermediate control point) and a closed (local surveillance of a specific territory with a return to the take-off point) trajectory pattern.

Fig. 7. UAV surveillance trajectory: I, II – open and closed trajectory pattern.

The generation of the i-th segment of the trajectory is a two-point problem, which depends on the available information about neighboring waypoints 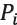acting as boundary conditions: coordinates, velocity and acceleration values at the initial and final time points on each segment. Thus, the spatial motion law can be represented by three parametrized time-dependent polynomials of 5-th order [9], [11], [22]:

Equation 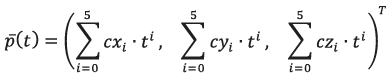18

(18)

Where:

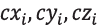- coefficients calculated from boundary conditions.

In this work, an open trajectory pattern is considered for further calculations and presentation of results. According to figure 7, the open trajectory pattern consists of three main stages: take off, cruise flight and landing. The first stage (takeoff) occurs from the point P₀ to P₁. The second stage (cruise flight) involves the UAV motion from the point P₁ to P₄, passing through the intermediate points P₂and P₃ respectively. The last stage (landing) is carried out from point P₄ to P₅.

It is known that the start of UAV flight from the ground occurs when the normal reaction generated on the UAV by the support surface 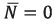, while the following condition is satisfied: 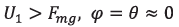. In addition, during the flight is necessary to orient the UAV relative to the given trajectory by the heading angle c (angle between the diametral plane of the aerial vehicle and the direction to the trajectory) turning around the UAV center of mass at the yaw angle y, and then adjusting the UAV position into an angle β, which is defined as the tangent of the inclination angle between the straight-line 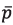and the OY axis (figure 8a). Therefore, the heading angle c turns equals to the yaw angle y. This correlation could be determined by the equation:

Equation 19

(19)

Where:

X₁, Y₁ - direction of the local coordinate system.

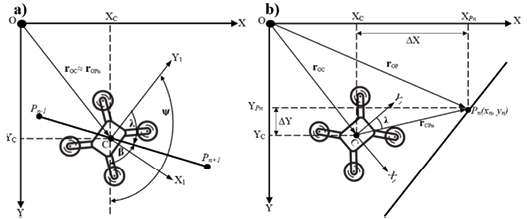
Fig. 8. UAV angle orientation scheme: a) heading angle correction λ, b) motion correction along the horizontal plane.

As mentioned before, the presence of external disturbances significantly affects the dynamics of the UAV flight, which leads to motion deviations from the desired trajectory (figure 8b). In this regard, it is proposed to carry out the return of the aerial vehicle to the desired trajectory by turning the UAV at heading angle c, and then calculate the path deviation vector according to the equation [11], [16]:

Equation 20

(20)

Where:

- vector representing the UAV path to the i-th point of given trajectory, 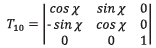- transformation matrix from local to global coordinate system.

III. Results and Discussion

In this section are presented the main results of the simulation process carried out in MATLAB for the UAV autonomously controlled motion in presence of external disturbances along an open trajectory pattern in terms of stabilization and positioning accuracy properties. The parameters of the trajectory pattern considered in Table I correspond to the coordinates of the waypoints 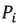(i = 1-5), time intervals and boundary conditions.

TABLE I. UAV Trajectory Desing Parameters

Based on the information about boundary conditions and equation 18, a vector of coefficients 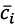is generated in concordance with the desired values for position 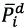, velocity 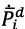and acceleration on each segment of the trajectory. In addition, the deviation vectors and control signals are determined at each iteration during the modeling process by integrating the differential equations of the UAV model, represented by the equation 11 using the Euler numerical integration method with a fixed step of 0.001s. Besides, during the simulation process parameters, such as dimensional, mass-inertial and electromechanical main characteristics of the UAV are considered (Table II).

TABLE II. UAV Parameters

At the first stage, the adequacy of the selected synthesis method of the controller operating by an adaptive PID based MPC control system during aerial surveillance missions must be performed. The main results are shown in figures 9 to 12.

Fig. 9. Diagrams of the UAV center of mass deviation from the desired coordinates: a, b, c – UAV displacement along OX, OY, OZ axes; d, e, f – variation of the aircraft angles j, q, y; I, II, III – take off, cruise flight and landing stages respectively.

Fig. 10. Diagrams of the UAV center of mass deviation from the desired angular orientation: a, b, c – UAV deviation relative to OX, OY, OZ axes by aircraft angles j, q, y; I, II, III – take off, cruise flight and landing stages respectively.

In figure 11 is presented a comparative analysis between PID and Adaptive PID based MPC control system capabilities in terms of stabilization and positioning accuracy properties during open loop trajectory pattern.

Fig. 11. 3D open trajectory pattern tracking

From results obtained in figures 9 to 11 becomes possible to state that the average deviation of the coordinates of the UAV center of mass along OX, OY, OZ axes is in range 0.025; 0.01 and 0.043 m, respectively. In addition, the average deviation from the UAV desired angular orientation corresponds to 0.08 rad. (relative to OX, OY axes) and 0.06 rad (relative to OZ axis). Therefore, the proposed control strategy ensures high accuracy in terms of positioning the UAV center of mass relative to a given trajectory by optimizing the vector of control signals 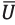(figure 12).

Fig. 12. Diagrams of the UAV controlled states: a – lift force ; b, c, d – external moments 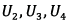along OX, OY, OZ axes respectively.

From figure 12 follows that the average value of the lifting force 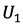is 18.43 N when changing the angular velocity of the i-th rotor in a range from 5042 to 5077 rpm, depending on the trajectory section and UAV maneuvers. In addition, the average value of the control signals 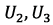is 0.03 Nm, while signal 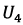varies in a range up to 0.06 Nm. Besides, the results confirm that the introduction of the MPC strategy suppresses jumps changes in 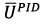parameters and provides smoother characteristics in transient process by optimizing the parameters of the controller. Thus, the UAV model can be used as a virtual simulator to study the influence of wind loads on the desired behavior and performance of the aerial platform during flight missions along coastal line. The simulation of wind loads behavior represents a complex task, which requires a set of observations corresponding to a certain time interval, climatic and geographical features of a specific area. With the aim to increase the reliability of the results of wind loads influence on UAV aerodynamics characteristics and adequacy of the designed control system during autonomous surveillance missions, a study of the UAV disturbed motion has been conducted considering a sample of several wind loads observations in the coastal territories of Ecuador. The information was extracted from the database of meteorological stations of the Oceanographic and Antarctic Institute of the Ecuadorian Navy, and National Institute of Meteorology and Hydrology [20], [21].

TABLE III. Non-deterministic Wind Load Parameters

At the first stage of the investigation, have been considered the non-deterministic wind load parameters described in Table III, as well as the continuous random function with normal Gaussian distribution of the equation 7. According to the results shown in figures 13 to 15 the distribution of the wind load in the specified time sections leads to a change in the nature of the deviation of the aircraft angles 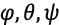in a range up to 0.2; 0.45 and 0.44 rad. Consequently, this affects the UAV positioning accuracy, resulting in deviations of 0.1; 0.28 and 0.13 m along each axis in the specified intervals.

Fig. 13. Diagram of the variation in the deviation of the UAV center of mass along the X axis: a – Wind load distribution along the X axis; b –deviation of the UAV movement along the X axis; c –deviation of the UAV center of mass by the pitch angle θ.

Fig. 14. Diagram of the variation in the deviation of the UAV center of mass along the Y axis: a – Wind load distribution along the Y axis; b –deviation of the UAV movement along the Y axis; c –deviation of the UAV center of mass by the roll angle φ.

Fig. 15. Diagram of the variation in the deviation of the UAV center of mass along the Z axis: a – Wind load distribution along the Z axis; b –deviation of the UAV movement along the Z axis; c –deviation of the UAV center of mass by the yaw angle ψ.

At the second stage of the investigation, the wind loads deterministic behavior is simulated according to the parameters described in Table IV, including equations 8 to 10.

TABLE IV. Deterministic Wind load Parameters

In accordance with the results presented in figures 16 to 18, the considered wind loads deterministic models represent a significant atmospheric disturbance on UAV performance. However, the UAV control system demonstrates the capability to maintain the center of mass positioning accuracy relative to the specified trajectory within deviations of 0.056; 0.36; 0.27 m along the OX, OY, OZ axes, respectively.

Fig. 16. Diagram of the variation in the deviation of the UAV center of mass along the X axis: a – wind load stepwise effect along X axis; b – deviation of the UAV movement along the X axis; c –deviation of the UAV center of mass by the pitch angle θ.

Fig. 17. Diagram of the variation in the deviation of the UAV center of mass along the Y axis: a – wind load stepwise effect along Y axis; b – deviation of the UAV movement along the Y axis; c –deviation of the UAV center of mass by the roll angle φ.

Fig. 18. Diagram of the variation in the deviation of the UAV center of mass along the Z axis: a – wind load stepwise effect along Z axis; b – deviation of the UAV movement along the Z axis; c –deviation of the UAV center of mass by the yaw angle ψ.

IV. Conclusions

This paper addresses the technical monitoring challenges faced by national security services in the coastal territories of Ecuador and proposes the use of an autonomous robotic aerial platform to enhance the efficiency of remote surveillance missions conducted along the coastline. The use of a hierarchical control structure, composed of an adaptive PID based MPC control strategy, optimizes the flight dynamics retaining UAV robust performance features. Based on the conducted study evaluating the influence of wind load disturbances on UAV controlled motion, it was revealed that deterministic models have a stronger effect on UAV flight dynamics. However, for both models (random and deterministic), the use of the Gaussian normal function and Fourier series decomposition method, respectively, represents a more reliable strategy for simulating the dynamics of air mass movement in a specific territory based on a priori information from meteorological service observations. The introduced wind disturbance models contribute to positioning accuracy deviations up to 0,1; 0,36; 0,27 m along OX, OY, OZ axes respectively. Additionally, a delay in the response of the control system to external disturbances at transient values of up to 5 seconds has been registered.

1 Associate professor, Faculty of Earth Sciences, Universidad Estatal Amazónica, Puyo 160150, Ecuador, and Researcher, Department of Mechanics, Mechatronics and Robotics, Southwest State University, Kursk 305040, Russia. (e-mail: amartinez@uea.edu.ec). ORCID number https://orcid.org/0000-0002-8598-7304.

2 Head of the Department of Mechanics, Mechatronics and Robotics, Southwest State University, Kursk 305040, Russia (email: teormeh@inbox.ru). ORCID number https://orcid.org/0000-0002-7420-0772.

3 Associate professor, Department of Mechanics, Mechatronics and Robotics, Southwest State University, Kursk 305040, Russia (email: oks-emelyanova@yandex.ru). ORCID number https://orcid.org/0000-0002-6067-3114.

References

[1] X. Wang, Z. Huang, G. Sui, H. Lian, “Analysis on the Development Trend of Future UAV Equipment Technology,” Academic Journal of Engineering and Technology Science, vol. 2, no. 1, pp. 114-121, 2020.

[2] A.S. Martinez, L.M. Mosquera, O. Emelyanova, “Control System of Small-Unmanned Aerial Vehicle for Monitoring Sea Vessels on Coastal Territory of Ecuador,” Frontiers in Robotics and Electromechanics, vol. 329, pp. 295-314, 2023.

[3] B. Fan, Y. Li, R. Zhang, Q. Fu, “Review on the Technological Development and Application of UAV systems”, Chinese Journal of Electronics, vol. 29, no. 2, pp. 199-207, 2020.

[4] S. Jatsun, O. Emelyanova, P. Bezmen, A. S. Martinez-León and L. M. Mosquera-Morocho, “Hardware/Software Architecture for Research of Control Algorithms of a Quadcopter in the Presence of External Wind Loads,” Electromechanics and Robotics, vol. 232, pp. 165-177, 2022.

[5] A. Correia, P.B. Água, R. Graça, “Machine Learning in Coastal Incident Detection, Identification and Classification with UAV’s,” in 16th Iberian Conference on Information Systems and Technologies (CISTI), 2021, pp. 1-6.

[6] D.R. Green, J. J. Hagon, C. Gómez, B. L. Gregory, “Using Low-Cost UAV’s for Environmental Monitoring, Mapping, and Modelling: Examples from the Coastal Zone,” Coastal management. Academic Press, pp. 465-501, 2019.

[7] M. Zurita, W. Aguilar, V. Enríquez, “Toward the Development of Surveillance and Reconnaissance Capacity in Ecuador: Geolocation System,” Developments and Advances in Defense and Security: Proceedings of MICRADS 2019, pp. 123-136, 2019.

[8] A. Flores, D. Scipión, C. Saito, J. Apaza, M. Milla, “Unmanned Aircraft System for Andean Volcano Monitoring and Surveillance,” in International Symposium on Safety, Security, and Rescue Robotics (SSRR), 2019, pp. 297-302.

[9] E. A. Valencia, K. A. Palma, I. D. Changoluisa, V. H. Hidalgo, P. J. Cruz, C. E. Cevallos, P. J. Ayala, D. F. Quisi, N. G. Jara, “Wetland Monitoring Through the Deployment of an Autonomous Aerial Platform,” IOP Conference Series: Earth and Environmental Science, vol. 32, no. 1, 012002, 2019.

[10] H. Loya, V. Enríquez, F. Salazar, C. Sánchez, F. Urrutia, J. Buele, “Analysis and Determination of Minimum Requirements of an Autopilot for the Control of Unmanned Aerial Vehicles (UAV),” in International Conference on Computer Science, Electronics and Industrial Engineering (CSEI), pp. 129-142, 2019.

[11] D. Mellinger, V. Kumar, “Control and Planning for Vehicles with Uncertainty in Dynamics,” IEEE International Conference on Robotics and Automation (ICRA), 2010, pp. 960-965.

[12] N. Bao, X. Ran, Z. Wu, Y. Xue, K. Wang, “Research on Attitude Controller of Quadcopter Based on Cascade PID Control Algorithm,” in IEEE Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), 2017, pp. 1493-1497.

[13] A. Zenkin, I. Berman, K. Pachkouski, I. Pantiukhin, V. Rzhevskiy, “Quadcopter Simulation Model for Research of Monitoring Tasks,” 26th Conference of Open Innovations Association, 2020, pp. 449-457.

[14] S. Jatsun, L.M. Mosquera-Morocho, O. Emelyanova, A. S. Martinez-León, “Controlled Adaptive Flight of a Convertiplane Type Tricopter in Conditions of Uncertainty for Monitoring Water Areas,” in 2020 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), 2020, pp. 1-7.

[15] I. Krzysztofik, Z. Koruba, “Analysis of Quadcopter Dynamics During Programmed Movement Under External Disturbance,” Nonlinear Dynamics and Control, pp. 177-185, 2020.

[16] S. Jatsun, O. Emelyanova, A.S. Martinez, “Design of an Experimental Test Bench for a UAV Type Convertiplane”, IOP Conference Series: Materials Science and Engineering, vol 714, no. 1, pp. 012009, 2020.

[17] A.S. Martinez, S. Jatsun, O. Emelyanova, “Control of the Electric Drives of a Multirotor System Type Convertertiplane,” Fundamental and Applied Problems of Technics and technology Journal, vol. 1, pp. 83-93, 2020.

[18] S. Jatsun, S. Efimov, O. Emelyanova, A. S. Martinez-León, P. J. Cruz-Dávalos, “Modeling and Control Architecture of an Autonomous Mobile Aerial Platform for Environmental Monitoring,” in 2019 International Conference on Information Systems and Computer Science (INCISCOS), pp. 177-182, 2019.

[19] O. Doukhi., A.R. Fayjie, D.J. Lee, “Intelligent Controller Design for Quadrotor Stabilization in Presence of Parameter Variations,” Journal of Advanced Transportation, 4683912, 2017.

[20] National Institute of Meteorology and Hydrology INAMHI, (2024, Feb 02) “Aplicativos Web”. [Online]. Available: https://inamhi.website/aplicaciones-web/

[21] Oceanographic and Antarctic Institute of the Ecuadorian Navy INOCAR, (2024, Feb 02) “Reporte Metereológico”. [Online]. Available: https://www.inocar.mil.ec/web/

[22] R. Casado, A. Bermúdez, “Simulation Framework for Developing Autonomous Drone Navigation Systems,” Electronics, 7, 2021.

[23] B. Lindqvist, S. S. Mansouri, A. Agha-Mohammadi, “Nonlinear MPC for Collision Avoidance and Control of UAV’s with Dynamic Obstacles,” Robotics and Automation Letters vol. 4, pp. 6001-6008, 2020.

[24] I. Nascimento, A. Ferramosca, L. Pimenta, G. Raffo, “NMPC Strategy for a Quadrotor UAV in a 3D Unknown Environment,” in 19th International Conference on Advanced Robotics (ICAR), pp. 179-184, 2019.

[25] A. Ryhlov, “Analysis of Different Distribution Laws Using for Wind Speed Leveling,” Proceedings of Saratov University: Earth Sciences Series, vol. 10, no. 2, pp. 25-30, 2010